Full message
# Author: Paul Fitzpatrick, paulfitz@alum.mit.edu # Copyright (c) 2018 Paul Fitzpatrick # # This file is part of CosmicOS. # # CosmicOS is free software; you can redistribute it and/or modify # it under the terms of the GNU General Public License as published by # the Free Software Foundation; either version 2 of the License, or # (at your option) any later version. # # CosmicOS is distributed in the hope that it will be useful, # but WITHOUT ANY WARRANTY; without even the implied warranty of # MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the # GNU General Public License for more details. # # You should have received a copy of the GNU General Public License # along with CosmicOS; if not, write to the Free Software # Foundation, Inc., 59 Temple Place, Suite 330, Boston, MA 02111-1307 USA #
0. introduce numbers (in unary notation)
Here we count up from zero, go through some primes, that sort of thing. Just like in the movies! There is some syntax around the numbers, and a structure to the “lesson,” but it will be fine for the listener to ignore all that for now. Hopefully what they will pick up on is:
- There are some repeating patterns.
- Between those patterns, there’s a specific short unit repeating a varying number of times (we count in unary).
- The number of times it varies smells like math.
We’ll get to a more compact representation of numbers later, once we’ve established the basics.
is int | unary 1 1 1 1 1 1 1 1 0;
is int | unary 1 1 1 1 1 1 1 1 1 0;
is int | unary 1 1 1 1 1 1 1 1 1 1 0;
is int | unary 1 1 1 1 1 1 1 1 1 1 1 0;
is int | unary 1 1 1 1 1 1 1 1 1 1 1 1 0;
is int | unary 1 1 1 1 1 1 1 1 1 1 1 1 1 0;
is int | unary 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0;
is int | unary 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0;
is square | unary 1 1 1 1 1 1 1 1 1 0;
is square | unary 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0;
is square | unary 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0;
is prime | unary 1 1 1 1 1 1 1 0;
is prime | unary 1 1 1 1 1 1 1 1 1 1 1 0;
is prime | unary 1 1 1 1 1 1 1 1 1 1 1 1 1 0;
is prime | unary 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0;
is prime | unary 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0;
is prime | unary 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0;
is prime | unary 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0;
is prime | unary 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0;
1. introduce equality and inequality of numbers
We’ve hopefully cued our listeners to be looking for mathematical patterns. So let’s give them some more. It doesn’t matter so much what patterns we give, as long as they are clear, and that there are several of them. Eventually we’ll want the listener to start turning things around, and use the parts of the message they understand (the mathematical patterns) to learn something about the parts they don’t (the message structure and syntax).
Let’s take a shot at introducing ways of comparing numbers. No doubt we’re revealing a feudal, reductive mindset in which all things must be ranked in a hierachy. ¯\_(ツ)_/¯.
Equality is introduced by a series of true statements of the form X = X
(the syntax is a little different than regular math, more like
= X X, but that isn’t important yet). The listener will hopefully
discern a number getting repeated twice within the “sentence”
structure they’ve been seeing, but won’t be sure yet what we are
driving at until we introduce non-equality and contrast with it.
= (unary 1 1 1 0) (unary 1 1 1 0);
= (unary 1 1 1 1 0) (unary 1 1 1 1 0);
= (unary 1 1 1 1 1 0) (unary 1 1 1 1 1 0);
= (unary 1 1 1 1 1 1 0) (unary 1 1 1 1 1 1 0);
= (unary 1 1 1 1 1 1 1 0) (unary 1 1 1 1 1 1 1 0);
= (unary 1 1 1 1 1 1 1 1 0) (unary 1 1 1 1 1 1 1 1 0);
= (unary 1 1 1 1 1 1 0) (unary 1 1 1 1 1 1 0);
Now introduce symbols for ‘greater than’ and ‘less than,’ and contrast with equality. Hopefully the listener will start to understand what part of the sentences are numbers, what part is a function of the relationship between the numbers, and what parts are just meaningless (for now) scaffolding around all that. There’s an ambiguity between the ‘greater than’ and ‘less than’ symbols, depending on how you interpret the sentences, but it doesn’t matter yet.
< (unary 1 0) (unary 1 1 1 1 0);
< (unary 1 1 0) (unary 1 1 1 0);
< (unary 1 1 0) (unary 1 1 1 1 0);
> (unary 1 1 1 0) (unary 1 1 0);
= (unary 1 1 1 0) (unary 1 1 1 0);
< (unary 1 1 1 0) (unary 1 1 1 1 0);
> (unary 1 1 1 1 0) (unary 1 0);
> (unary 1 1 1 1 0) (unary 1 1 0);
> (unary 1 1 1 1 0) (unary 1 1 1 0);
= (unary 1 1 1 1 0) (unary 1 1 1 1 0);
Add some random examples.
> (unary 1 1 1 1 0) (unary 1 1 1 0);
> (unary 1 1 1 1 1 1 1 1 0) (unary 0);
> (unary 1 1 1 1 1 1 1 0) (unary 1 1 1 1 1 1 0);
> (unary 1 1 1 1 1 1 0) (unary 1 1 0);
> (unary 1 1 1 1 1 0) (unary 0);
> (unary 1 1 1 1 1 1 1 1 1 0) (unary 1 1 1 1 0);
> (unary 1 1 1 1 1 0) (unary 1 0);
< (unary 1 1 1 1 1 1 1 0) (unary 1 1 1 1 1 1 1 1 1 0);
< (unary 1 1 1 0) (unary 1 1 1 1 1 1 0);
< (unary 1 1 0) (unary 1 1 1 0);
< (unary 1 1 0) (unary 1 1 1 1 0);
< (unary 0) (unary 1 1 1 1 1 1 1 1 1 1 0);
< (unary 1 1 1 1 0) (unary 1 1 1 1 1 1 0);
< (unary 1 0) (unary 1 1 1 1 1 1 1 1 0);
Even more random examples. We shouldn’t be shy about piling on examples at this early stage of the message. Even just the repetition of the sentence structure with many small variations could help guide the listener at a more fundamental level than what we’re ostensibly trying to communicate here.
= (unary 1 1 1 1 0) (unary 1 1 1 1 0);
> (unary 1 1 1 1 0) (unary 1 1 0);
> (unary 1 1 1 0) (unary 1 1 0);
< (unary 1 1 1 0) (unary 1 1 1 1 0);
> (unary 1 1 1 0) (unary 1 1 0);
> (unary 1 1 1 1 0) (unary 1 1 0);
< (unary 1 1 0) (unary 1 1 1 1 0);
< (unary 1 0) (unary 1 1 1 1 0);
> (unary 1 1 1 1 0) (unary 1 1 1 0);
< (unary 1 1 0) (unary 1 1 1 1 0);
< (unary 1 1 0) (unary 1 1 1 1 0);
2. introduce logical negation
At this point, the listener can find numbers in our sentences, and has some idea of symbols related to equality and inequality. But the structure of the sentences remains a mystery. Let’s introduce more math, so that we can show different sentence structures. First, let’s introduce logical negation. We construct some sentences the listener should know are wrong, and put “not” in front of them.
Show an equality, then negate two conflicting inequalities.
= (unary 1 1 1 1 0) (unary 1 1 1 1 0);
not | < (unary 1 1 1 1 0) (unary 1 1 1 1 0);
not | > (unary 1 1 1 1 0) (unary 1 1 1 1 0);
= (unary 1 1 1 1 1 1 0) (unary 1 1 1 1 1 1 0);
not | < (unary 1 1 1 1 1 1 0) (unary 1 1 1 1 1 1 0);
not | > (unary 1 1 1 1 1 1 0) (unary 1 1 1 1 1 1 0);
not | < (unary 1 1 0) (unary 1 1 0);
not | > (unary 1 1 0) (unary 1 1 0);
= (unary 1 1 1 0) (unary 1 1 1 0);
not | < (unary 1 1 1 0) (unary 1 1 1 0);
not | > (unary 1 1 1 0) (unary 1 1 1 0);
Show an inequality, then two negations.
< (unary 1 1 1 0) (unary 1 1 1 1 1 1 1 1 1 1 0);
not | = (unary 1 1 1 0) (unary 1 1 1 1 1 1 1 1 1 1 0);
not | > (unary 1 1 1 0) (unary 1 1 1 1 1 1 1 1 1 1 0);
< (unary 1 1 1 1 1 0) (unary 1 1 1 1 1 1 1 0);
not | = (unary 1 1 1 1 1 0) (unary 1 1 1 1 1 1 1 0);
not | > (unary 1 1 1 1 1 0) (unary 1 1 1 1 1 1 1 0);
not | = (unary 1 0) (unary 1 1 0);
not | > (unary 1 0) (unary 1 1 0);
< (unary 0) (unary 1 1 1 1 1 0);
not | = (unary 0) (unary 1 1 1 1 1 0);
not | > (unary 0) (unary 1 1 1 1 1 0);
< (unary 1 1 1 1 1 1 1 1 0) (unary 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0);
not | = (unary 1 1 1 1 1 1 1 1 0) (unary 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0);
not | > (unary 1 1 1 1 1 1 1 1 0) (unary 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0);
Show another batch of inequalities with negations.
> (unary 1 1 1 1 1 1 1 1 1 1 1 0) (unary 1 1 1 1 1 1 0);
not | = (unary 1 1 1 1 1 1 1 1 1 1 1 0) (unary 1 1 1 1 1 1 0);
not | < (unary 1 1 1 1 1 1 1 1 1 1 1 0) (unary 1 1 1 1 1 1 0);
> (unary 1 1 1 1 1 1 1 1 1 1 1 1 0) (unary 1 1 0);
not | = (unary 1 1 1 1 1 1 1 1 1 1 1 1 0) (unary 1 1 0);
not | < (unary 1 1 1 1 1 1 1 1 1 1 1 1 0) (unary 1 1 0);
> (unary 1 1 1 1 1 1 1 1 1 1 0) (unary 1 1 1 1 1 1 1 0);
not | = (unary 1 1 1 1 1 1 1 1 1 1 0) (unary 1 1 1 1 1 1 1 0);
not | < (unary 1 1 1 1 1 1 1 1 1 1 0) (unary 1 1 1 1 1 1 1 0);
not | = (unary 1 1 1 1 0) (unary 0);
not | < (unary 1 1 1 1 0) (unary 0);
> (unary 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0) (unary 1 1 1 1 1 1 1 1 1 0);
not | = (unary 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0) (unary 1 1 1 1 1 1 1 1 1 0);
not | < (unary 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0) (unary 1 1 1 1 1 1 1 1 1 0);
3. introduce addition
Let’s introduce some arithmetic, to show off still more sentence structure.
We show sentences of the mathematical form X = Y + Z, which in our message look like
= X | + Y Z. From this, and the negation lesson, the listener will hopefully
start picking up on how to chain operations.
If the listener didn’t already have a pretty clear idea of what = is,
then these sentences could just as easily be interpreted as being about subtraction.
Even having an idea of =, syntax is still fuzzy enough that this lesson may not
be unambiguous by itself.
= (unary 1 1 0) | + (unary 0) (unary 1 1 0);
= (unary 1 1 1 1 1 0) | + (unary 1 1 1 1 0) (unary 1 0);
= (unary 1 1 0) | + (unary 1 1 0) (unary 0);
= (unary 1 1 1 1 0) | + (unary 0) (unary 1 1 1 1 0);
= (unary 1 1 1 1 0) | + (unary 1 1 1 0) (unary 1 0);
= (unary 1 1 1 0) | + (unary 1 0) (unary 1 1 0);
= (unary 0) | + (unary 0) (unary 0);
= (unary 1 1 1 1 0) | + (unary 1 1 1 1 0) (unary 0);
= (unary 1 1 1 0) | + (unary 1 1 0) (unary 1 0);
= (unary 1 1 1 1 0) | + (unary 1 1 1 1 0) (unary 0);
4. introduce subtraction
Introduce subtraction via = X | - Y Z sentences. Until syntax is fully understood,
an ambiguity may remain between this and addition.
= (unary 0) | - (unary 1 1 0) (unary 1 1 0);
= (unary 1 1 1 1 0) | - (unary 1 1 1 1 1 0) (unary 1 0);
= (unary 1 1 0) | - (unary 1 1 0) (unary 0);
= (unary 0) | - (unary 1 1 1 1 0) (unary 1 1 1 1 0);
= (unary 1 1 1 0) | - (unary 1 1 1 1 0) (unary 1 0);
= (unary 1 0) | - (unary 1 1 1 0) (unary 1 1 0);
= (unary 0) | - (unary 0) (unary 0);
= (unary 1 1 1 1 0) | - (unary 1 1 1 1 0) (unary 0);
= (unary 1 1 0) | - (unary 1 1 1 0) (unary 1 0);
= (unary 1 1 1 1 0) | - (unary 1 1 1 1 0) (unary 0);
5. introduce multiplication
While we’re at it, let’s introduce multiplication with = X | * Y Z sentences.
As for addition and subtraction, there will be some ambiguity as to whether we are
presenting multiplication or division here, until syntax is clearly understood.
= (unary 0) | * (unary 0) (unary 0);
= (unary 0) | * (unary 0) (unary 1 0);
= (unary 0) | * (unary 0) (unary 1 1 0);
= (unary 0) | * (unary 0) (unary 1 1 1 0);
= (unary 0) | * (unary 1 0) (unary 0);
= (unary 1 0) | * (unary 1 0) (unary 1 0);
= (unary 1 1 0) | * (unary 1 0) (unary 1 1 0);
= (unary 1 1 1 0) | * (unary 1 0) (unary 1 1 1 0);
= (unary 0) | * (unary 1 1 0) (unary 0);
= (unary 1 1 0) | * (unary 1 1 0) (unary 1 0);
= (unary 1 1 1 1 0) | * (unary 1 1 0) (unary 1 1 0);
= (unary 1 1 1 1 1 1 0) | * (unary 1 1 0) (unary 1 1 1 0);
= (unary 0) | * (unary 1 1 1 0) (unary 0);
= (unary 1 1 1 0) | * (unary 1 1 1 0) (unary 1 0);
= (unary 1 1 1 1 1 1 0) | * (unary 1 1 1 0) (unary 1 1 0);
= (unary 1 1 1 1 1 1 1 1 1 0) | * (unary 1 1 1 0) (unary 1 1 1 0);
= (unary 0) | * (unary 0) (unary 1 0);
= (unary 1 1 1 0) | * (unary 1 1 1 0) (unary 1 0);
= (unary 0) | * (unary 1 1 0) (unary 0);
= (unary 0) | * (unary 0) (unary 1 1 1 0);
= (unary 1 1 1 0) | * (unary 1 1 1 0) (unary 1 0);
= (unary 1 1 0) | * (unary 1 0) (unary 1 1 0);
= (unary 0) | * (unary 0) (unary 0);
= (unary 0) | * (unary 1 1 1 0) (unary 0);
= (unary 0) | * (unary 1 1 0) (unary 0);
= (unary 0) | * (unary 1 1 1 0) (unary 0);
6. introduce non-unary representation of numbers
Switch from unary numbers to another representation. The best representation will depend on the details of how the message is being transmitted, and the rest of the message doesn’t depend on that choice for correctness (though the choice will have implications for how easy the message will be to interpret). As a base-line, imagine we use a binary representation.
It isn’t important for the listener to understand, but it might be worth explaining at this point how the unary representation worked. In fact there’s no special syntax used, just three objects:
- The number
0. - The number
1. - A function (called
unaryin English) that takes a value and:- If passed
0, the function returns0 - If passed
1, the function returns another function, just like itself, except with any ultimate return value increased by1.
- If passed
Using syntax defined later in the message, unary could be defined as:
@ unary-v | ? v | ? x | if (= $x 0) $v (unary-v | + $v 1)
@ unary | unary-v 0
If you know Lisp/Scheme/etc, just read @ as define, ? as
lambda, and | as opening a parenthesis that gets closed at the end
of the statement.
Anyway, all of this is a digression, but it is worth knowing that as much as possible the message is built from itself, so that in the end everything dovetails nicely.
= 8 (unary 1 1 1 1 1 1 1 1 0);
= 9 (unary 1 1 1 1 1 1 1 1 1 0);
= 10 (unary 1 1 1 1 1 1 1 1 1 1 0);
= 11 (unary 1 1 1 1 1 1 1 1 1 1 1 0);
= 12 (unary 1 1 1 1 1 1 1 1 1 1 1 1 0);
= 13 (unary 1 1 1 1 1 1 1 1 1 1 1 1 1 0);
= 14 (unary 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0);
= 15 (unary 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0);
= 8 (unary 1 1 1 1 1 1 1 1 0);
= 16 (unary 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0);
= 14 (unary 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0);
= 13 (unary 1 1 1 1 1 1 1 1 1 1 1 1 1 0);
= 11 (unary 1 1 1 1 1 1 1 1 1 1 1 0);
= 9 (unary 1 1 1 1 1 1 1 1 1 0);
= 15 (unary 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0);
= 8 (unary 1 1 1 1 1 1 1 1 0);
= 12 (unary 1 1 1 1 1 1 1 1 1 1 1 1 0);
= 10 (unary 1 1 1 1 1 1 1 1 1 1 0);
= (unary 1 1 1 1 1 1 1 1 1 0) | + (unary 1 1 1 1 1 1 0) (unary 1 1 1 0);
= (unary 1 1 1 1 1 1 0) | + (unary 0) (unary 1 1 1 1 1 1 0);
= (unary 1 1 1 1 1 1 1 1 1 1 0) | + (unary 1 1 1 1 1 1 0) (unary 1 1 1 1 0);
= (unary 1 1 1 1 1 0) | + (unary 1 1 1 0) (unary 1 1 0);
= (unary 1 0) | + (unary 1 0) (unary 0);
= (unary 1 1 1 1 1 1 0) | + (unary 1 1 0) (unary 1 1 1 1 0);
= (unary 1 1 1 1 1 1 1 1 1 1 1 1 0) | + (unary 1 1 1 1 1 1 0) (unary 1 1 1 1 1 1 0);
= (unary 1 1 1 1 1 1 1 1 0) | + (unary 1 1 1 1 0) (unary 1 1 1 1 0);
= (unary 0) | * (unary 0) (unary 1 1 0);
= (unary 1 1 0) | * (unary 1 0) (unary 1 1 0);
= (unary 0) | * (unary 0) (unary 1 0);
= (unary 0) | * (unary 1 1 1 0) (unary 0);
= (unary 0) | * (unary 0) (unary 0);
= (unary 0) | * (unary 1 0) (unary 0);
= (unary 1 1 1 1 0) | * (unary 1 1 0) (unary 1 1 0);
= (unary 1 1 1 1 1 1 1 1 1 0) | * (unary 1 1 1 0) (unary 1 1 1 0);
7. show alternative groupings
We’ve advanced enough that we’re starting to have choices about how something is expressed. Let’s pause to acknowledge that, and reinforce some syntactic equivalences so the listener can be confident of them.
Parentheses play a role in grouping expressions, just like in regular
math. To reduce the mental burden of tracking nesting, we use a | shortcut
that means “add parentheses between this point and as far as you can go.” So for
example (= 7 | + 3 4) is equivalent to (= 7 (+ 3 4)).
8. show local assignment
An expression starting with assign is a way to name values for use within that expression. To use the assigned value, simply place its name at the beginning of an expression. For example, a value assigned to x can be used by writing (x). The name is entirely arbitrary, and can be just an integer.
assign x 1 | assign y 2 | = 3 (+ (x) (y));
assign x 2 | assign y 7 | = 5 (- (y) (x));
assign x (+) | assign y 3 | = 4 (x 1 (y));
We are pretty ruthless about adding syntax to reduce parentheses. So let’s allow writing (x) as $x (or equivalent in other renderings). This and | are in fact global options for the message that you can turn off if they are not to your taste.
Add more examples to give hints about scoping and other odd corners.
= 4 | assign x (assign y 3 | + 1 $y) $x;
= 4 | assign x (assign x 3 | + 1 $x) $x;
We’re ready for functions. ? starts a lambda function. Now we can have fun!
Emphasize the arbitrary nature of names, and hint that things we’ve learned already like addition could possibly be re-imagined as a named value.
Show that we can name functions and use them later - still within a single expression for now.
assign x (? y | * $y $y) | = 25 | x 5;
assign x (? y | + $y 1) | = 6 | x 5;
assign x (? x | + $x 1) | = 6 | x 5;
assign y (? x | + $x 1) | = 6 | y 5;
Show that we can nest functions to take multiple values.
= 52 | (? x | ? y | * $x $y) 13 4;
= 53 | (? x | ? y | + 1 | * $x $y) 13 4;
assign z (? x | ? y | + 1 | * $x $y) | = 53 | z 13 4;
9. demonstrate existence of memory
We’ve set up a way to name a value within an expression. Now let’s go beyond that, and introduce a way to name a value in one sentence and use it in a later sentence. In other words, a message-level memory. After this, we’ll be able to define new symbols from existing ones, with less need for large numbers of examples.
We introduce a define symbol that works just like assign, except that it applies
to the rest of the message rather than the rest of the sentence.
A sentence of the form define X Y means that $X will evaluate to Y from that
point on (unless X is changed by another define).
The meaning-of-life-universe-everything symbol here is entirely arbitrary, and
won’t be encoded as anything particularly meaningful in the message.
= 49 | + 10 $meaning-of-life-universe-everything;
= 80 | * $meaning-of-life-universe-everything 2;
define meaning-of-life-universe-everything | + 1 $meaning-of-life-universe-everything;
assign x (+ 1 $meaning-of-life-universe-everything) | define meaning-of-life-universe-everything $x;
Now we can start defining and naming functions. Here’s one to square an integer.
Here’s a function to increment an integer.
10. introduce true and false
Now that we have functions, we could introduce some clever definitions of true, false, and conditionals, where:
ifis? x | ? y | ? z | x $y $ztrueis? y | ? z | yfalseis? y | ? z | z
This is a neat implementation, but maybe a bit confusing. So let’s
not actually commit to a type for truth values in the message yet,
but just equate them with the results of equality =.
Once we have truth values, we can introduce conditionals and build up to fun stuff.
One slightly sneaky thing we do is to code true and false as $1
and $0. This could be helpful, or confusing, I’m not sure. Nothing
else in the message depends on this so it can be adjusted to taste.
11. show conditionals
Now that we spent some time looking at true and false, let’s show
a way to build conditional expressions. We start with an if expression,
of the form if CONDITION E1 E2, which evaluates to E1 if the CONDITION
is true, otherwise E2.
If the listener is trying to map the language we are describing onto
their own system of computation, it is pretty important that if be
“lazy,” and completely skip evaluating the branch not taken. That
should become clear fairly soon if they were to try an “eager” if.
We can now define more interesting functions. Here’s the maximum of two integers:
define max | ? x | ? y | if (> $x $y) $x $y;
Now the minimum of two integers:
define min | ? x | ? y | if (< $x $y) $x $y;
Why should human CS students be the only ones the factorial example is inflicted on…
define factorial | ? x | if (< $x 1) 1 | * $x | factorial | - $x 1;
12. introduce the AND logical operator
We continue introducing symbols related to math and logic. Now we will often be able to both define them and give examples, so the listener has multiple paths to understanding.
Here is and, which evaluates to true if both its two arguments are true,
and false otherwise. We don’t talk about wbat happens if you pass it integers
or something funky. There’d be value in getting into talking about types, but
it might be a bit much just now.
define and | ? x | ? y | if $x $y $false;
13. introduce the OR logical operator
Here is or, which evaluates to true if either of its arguments are true,
and false otherwise. Again, we just don’t talk about what happens if you
pass in any unexpected values, like integers or functions. The message is
constructed so that the problem never comes up.
define or | ? x | ? y | if $x $true $y
Now is an opportune moment to add <= and >= definitions.
There are shorter definitions, like just negating > and <, but this feels more natural?
define >= | ? x | ? y | or (> $x $y) (= $x $y);
define <= | ? x | ? y | or (< $x $y) (= $x $y);
14. introduce pairs
Now we introduce our first data structure. The expression cons X Y stores X and Y
in a pair. We can then pull X out from the pair with car (cons X Y), and we can
get Y out from the pair with cdr (cons X Y). Apologies for the arcane names,
they are inherited from Lisp (and they’ll be encoded as something else in the
message anyway).
We give a definition of cons that is a bit funky. The cons X Y expression
constructs a function which takes a single argument, also a function. That
argument gets called with X and Y. That means to pull X back out, we
just need to call cons X Y with a function like ? a | ? b $a. Likewise for
Y. That is exactly what car and cdr do.
Definitions like that can be a bit hard to think about. But the great thing is that you can apply definitions like these without initially understanding them. So if the listener wants to try them out, they can there’s an element of interactivity beyond what a plain text message could give.
define cons | ? x | ? y | ? z | z $x $y;
define car | ? z | z | ? x | ? y $x;
define cdr | ? z | z | ? x | ? y $y;
assign x (cons 0 4) | = 0 | car $x;
assign x (cons 0 4) | = 4 | cdr $x;
assign x (cons 6 2) | = 6 | car $x;
assign x (cons 6 2) | = 2 | cdr $x;
assign x (cons 3 9) | = 3 | car $x;
assign x (cons 3 9) | = 9 | cdr $x;
assign x (cons 7 | cons 10 2) | = 7 | car $x;
assign x (cons 7 | cons 10 2) | = 10 | car | cdr $x;
assign x (cons 7 | cons 10 2) | = 2 | cdr | cdr $x;
assign x (cons 1 | cons 15 17) | = 1 | car $x;
assign x (cons 1 | cons 15 17) | = 15 | car | cdr $x;
assign x (cons 1 | cons 15 17) | = 17 | cdr | cdr $x;
assign x (cons 8 | cons 14 9) | = 8 | car $x;
assign x (cons 8 | cons 14 9) | = 14 | car | cdr $x;
assign x (cons 8 | cons 14 9) | = 9 | cdr | cdr $x;
assign x (cons 3 | cons 0 | cons 2 | cons 4 1) | = 3 | car $x;
assign x (cons 3 | cons 0 | cons 2 | cons 4 1) | = 0 | car | cdr $x;
assign x (cons 3 | cons 0 | cons 2 | cons 4 1) | = 2 | car | cdr | cdr $x;
assign x (cons 3 | cons 0 | cons 2 | cons 4 1) | = 4 | car | cdr | cdr | cdr $x;
assign x (cons 3 | cons 0 | cons 2 | cons 4 1) | = 1 | cdr | cdr | cdr | cdr $x;
15. introduce mutable cells
With define, we showed that there is a global memory, where we can associate a
symbol with a value. That’s nice, but it can be handy to separate memory from
naming. In this section we introduce make-cell X, which creates a “cell”
of memory and puts X in it. The cell can be read with get!, like
get! | make-cell X, or written to with set!, like set! (make-cell-X) Y.
= 29 (+ (get! $demo:make-cell:x) | get! $demo:make-cell:y);
if (= (get! $demo:make-cell:x) 7) (set! $demo:make-cell:x 88) (set! $demo:make-cell:x 99);
if (= (get! $demo:make-cell:x) 7) (set! $demo:make-cell:x 88) (set! $demo:make-cell:x 99);
16. introduce lists
Lists are a handy data structure to have. We’d like to get to the point
in the message where we can make lists like this: vector 1 4 5,
vector 77 $undefined (vector 1 2 3) 14, etc. But
vector can’t be a function in the language we’ve described up to now,
it just can’t work syntactically.
What we can do is make lists like this: (list 3) 1 4 5,
(list 4) 77 $undefined ((list 3) 1 2 3) 14, where we manually
specify how many values are in the list.
And then we can introduce a way to transform the syntax of the language,
so that vector 1 4 5 gets rewritten to (list 3) 1 4 5 prior to being
evaluated.
An alternative would be just to introduce some special new syntax for
lists, and give examples. If the listener finds our transformation approach
confusing, they can simply ignore it and pick the message up again once
vector is in place. But by giving the transformation, we offer a second
way to understand and experiment with the concepts being introduced.
define list:n | ? n | ? ret | if (= $n 1) (? x | ret 1 $x) | ? x | list:n (- $n 1) | ? y | ? z | ret (+ 1 $y) | cons $x $z;
define list | ? n | if (= $n 0) (cons 0 0) (list:n $n $cons);
define head | ? x:list | if (= 0 | car $x:list) $undefined | if (= 1 | car $x:list) (cdr $x:list) | car | cdr $x:list;
define tail | ? x:list | if (= 0 | car $x:list) $undefined | if (= 1 | car $x:list) (cons 0 0) | cons (- (car $x:list) 1) | cdr | cdr $x:list;
= 14 | head | (list 9) 14 0 12 19 11 9 8 0 17;
= 16 | head | (list 6) 16 9 0 17 17 10;
= 5 | head | (list 5) 5 3 1 5 11;
= 15 | head | (list 9) 15 10 12 4 13 6 13 1 6;
= 4 | head | tail | (list 10) 1 4 3 7 0 1 2 11 13 3;
= 3 | head | tail | (list 5) 15 3 19 16 17;
= 8 | head | tail | (list 6) 6 8 13 9 18 2;
= 3 | head | tail | (list 8) 5 3 10 13 2 8 6 12;
= 11 | head | tail | (list 10) 14 11 18 9 9 11 3 10 16 2;
= 16 | head | tail | tail | (list 7) 19 7 16 17 12 1 18;
= 18 | head | tail | tail | (list 6) 16 9 18 5 11 17;
= 15 | head | tail | tail | (list 4) 1 0 15 18;
= 4 | head | tail | tail | (list 6) 0 0 4 19 1 5;
= 7 | head | tail | tail | (list 4) 7 1 7 14;
= 4 | list-length | (list 4) 1 9 3 6;
= 9 | list-length | (list 9) 6 2 5 8 7 4 1 3 0;
= 7 | list-length | (list 7) 6 0 1 9 4 5 2;
= 6 | list-length | (list 6) 2 4 7 0 3 8;
define list-ref | ? x:list | ? n | if (= 0 | car $x:list) $undefined | if (= $n 0) (head $x:list) | list-ref (tail $x:list) | - $n 1;
= 15 | list-ref ((list 4) 5 8 15 3) 2;
= 7 | list-ref ((list 7) 12 19 0 15 1 8 7) 6;
= 13 | list-ref ((list 4) 11 10 13 8) 2;
= 2 | list-ref ((list 6) 9 2 9 8 10 12) 1;
= 7 | list-ref ((list 4) 18 7 12 13) 1;
= 2 | list-ref ((list 9) 3 3 5 6 2 16 10 1 1) 4;
= 13 | list-ref ((list 7) 11 13 9 12 5 7 5) 1;
= 17 | list-ref ((list 9) 13 17 14 16 0 2 9 3 5) 1;
= 1 | list-ref ((list 9) 18 10 4 1 17 18 8 8 8) 3;
define equal | ? x | ? y | if (not | = (function? $x) (function? $y)) $false | if (function? $x) (list= $x $y) (= $x $y);
define list= | ? x | ? y | if (not | = (list-length $x) (list-length $y)) $false | if (= 0 | list-length $x) $true | if (not | equal (head $x) (head $y)) $false | list= (tail $x) (tail $y);
equal ((list 2) 5 3) ((list 2) 5 3);
not | equal ((list 2) 5 3) ((list 3) 5 3 9);
not | equal ((list 2) 5 3) ((list 2) 5 4);
not | equal ((list 2) 5 3) ((list 2) 4 3);
equal ((list 3) 5 3 9) ((list 3) 5 3 9);
equal ((list 3) 5 ((list 2) 15 1) 9) ((list 3) 5 ((list 2) 15 1) 9);
not | equal ((list 3) 5 ((list 2) 15 1) 9) ((list 3) 5 ((list 2) 14 1) 9);
not | equal ((list 3) 5 3 9) ((list 3) 5 ((list 2) 14 1) 9);
= (head | (list 8) 7 15 18 11 13 0 13 6) 7;
list= (tail | (list 8) 7 15 18 11 13 0 13 6) ((list 7) 15 18 11 13 0 13 6);
= (head | (list 9) 7 17 11 10 1 3 18 13 5) 7;
list= (tail | (list 9) 7 17 11 10 1 3 18 13 5) ((list 8) 17 11 10 1 3 18 13 5);
= (head | (list 7) 0 15 15 10 12 2 4) 0;
list= (tail | (list 7) 0 15 15 10 12 2 4) ((list 6) 15 15 10 12 2 4);
= (head | (list 5) 18 12 3 18 8) 18;
list= (tail | (list 5) 18 12 3 18 8) ((list 4) 12 3 18 8);
list= (tail | (list 2) 17 13) ((list 1) 13);
= (head | (list 5) 5 6 1 19 13) 5;
list= (tail | (list 5) 5 6 1 19 13) ((list 4) 6 1 19 13);
= (head | (list 9) 5 1 6 14 6 15 4 16 5) 5;
list= (tail | (list 9) 5 1 6 14 6 15 4 16 5) ((list 8) 1 6 14 6 15 4 16 5);
list= (tail | (list 4) 16 8 6 18) ((list 3) 8 6 18);
list= (tail | (list 3) 9 1 1) ((list 2) 1 1);
= (head | (list 4) 11 16 11 2) 11;
list= (tail | (list 4) 11 16 11 2) ((list 3) 16 11 2);
define prepend | ? x | ? x:list | cons (+ (car $x:list) 1) (if (= (car $x:list) 0) $x | cons $x | cdr $x:list);
list= (prepend 14 | (list 0)) ((list 1) 14);
list= (prepend 6 | (list 1) 4) ((list 2) 6 4);
list= (prepend 19 | (list 2) 17 14) ((list 3) 19 17 14);
list= (prepend 13 | (list 3) 12 7 16) ((list 4) 13 12 7 16);
list= (prepend 4 | (list 4) 15 18 6 10) ((list 5) 4 15 18 6 10);
list= (prepend 8 | (list 5) 2 19 15 13 13) ((list 6) 8 2 19 15 13 13);
list= (prepend 11 | (list 6) 0 17 15 4 10 7) ((list 7) 11 0 17 15 4 10 7);
list= (prepend 15 | (list 7) 2 12 18 12 4 1 12) ((list 8) 15 2 12 18 12 4 1 12);
define first | ? x:list | head $x:list;
define second | ? x:list | head | tail $x:list;
17. introduce map and reduce
For programming and for math, it is handy to be able to apply an element-wise transform to a list, and some kind of accumulator to pull out a summary.
define map | ? x:? | ? x:list | if (= 0 | list-length $x:list) (list 0) | prepend (x:? | head $x:list) (map $x:? | tail $x:list);
list= ((list 3) 12 34 6) | map (? x | * $x 2) | (list 3) 6 17 3;
list= ((list 4) 34 20 14 8) | map (? x | * $x 2) | (list 4) 17 10 7 4;
list= ((list 5) 8 4 16 0 6) | map (? x | * $x 2) | (list 5) 4 2 8 0 3;
list= ((list 6) 36 4 28 10 6 20) | map (? x | * $x 2) | (list 6) 18 2 14 5 3 10;
list= ((list 3) 42 42 42) | map (? x 42) | (list 3) 16 2 11;
list= ((list 4) 42 42 42 42) | map (? x 42) | (list 4) 15 18 6 0;
list= ((list 5) 42 42 42 42 42) | map (? x 42) | (list 5) 19 11 5 17 2;
list= ((list 6) 42 42 42 42 42 42) | map (? x 42) | (list 6) 11 19 5 3 12 6;
define reduce | ? x:? | ? x:list | if (= 0 | list-length $x:list) $undefined | if (= 1 | list-length $x:list) (head $x:list) | x:? (head $x:list) (reduce $x:? | tail $x:list);
= 21 | reduce $+ | (list 3) 3 7 11;
= 43 | reduce $+ | (list 4) 13 11 19 0;
= 41 | reduce $+ | (list 5) 9 2 10 8 12;
= 50 | reduce $+ | (list 6) 10 1 2 12 14 11;
18. how to change the imagined interpreter
define translate | ? x | if (= $x 32) 64 | translate:begin $x;
Now let’s do something useful: define a special form for lists.
define translate | ? x | if (not | function? $x) (translate:begin $x) | if (not | = vector | head $x) (translate:begin $x) | translate | prepend ((list 2) list | list-length | tail $x) | tail $x;
list= (vector 1 2 3) | (list 3) 1 2 3;
19. some more list functions
define list:find:0 | ? x:list | ? y | ? n | if (= (list-length $x:list) 0) $undefined | if (equal (head $x:list) $y) $n | list:find:0 (tail $x:list) $y (+ $n 1);
define list:find | ? x:list | ? y | list:find:0 $x:list $y 0;
= (list:find ((list 4) 17 4 3 0) 0) 3;
= (list:find ((list 8) 0 12 19 11 9 8 0 17) 9) 4;
= (list:find ((list 9) 9 0 17 17 10 8 5 3 1) 17) 2;
= (list:find ((list 6) 17 15 10 12 4 13) 15) 1;
= (list:find ((list 7) 1 6 18 1 4 3 7) 1) 0;
= (list:find ((list 7) 3 7 15 3 19 16 17) 3) 0;
= (list:find ((list 4) 8 13 9 18) 8) 0;
= (list:find ((list 8) 5 3 10 13 2 8 6 12) 12) 7;
= (list:find ((list 8) 11 18 9 9 11 3 10 16) 18) 1;
= (list:find ((list 4) 19 6 15 16) 11) $undefined;
= (list:find ((list 6) 0 1 5 19 2 8) 7) $undefined;
= (list:find ((list 8) 18 2 17 7 12 3 11 8) 6) $undefined;
define last | ? x | list-ref $x | - (list-length $x) 1;
define except-last | ? x | if (>= 1 | list-length $x) (vector) | prepend (head $x) | except-last | tail $x;
list= (vector 4 5) | except-last | vector 4 5 15;
define list:reverse | ? x:list | if (<= (list-length $x:list) 1) $x:list | prepend (last $x:list) | list:reverse | except-last $x:list;
list= (list:reverse | vector 1 2 3) (vector 3 2 1);
list= (list:reverse | vector 50 1 33 99) (vector 99 33 1 50);
define append | ? x | ? lst | if (= 0 | list-length $lst) (vector $x) | prepend (head | $lst) | append $x | tail $lst;
list= (vector 1 2 5) | append 5 | vector 1 2;
define select-match | ? test | ? lst | if (= 0 | list-length $lst) $lst | if (not | test | head $lst) (select-match $test | tail $lst) | prepend (head $lst) (select-match $test | tail $lst);
list= (vector 14 19 13) | select-match (? x | > $x 10) | vector 1 14 19 3 13 0 4;
20. introduce pi and e
Just in passing, give approximate values for pi and e.
define abs | ? x | if (> $x 0) $x (- 0 $x);
define within | ? epsilon | ? x | ? y | < (abs | - $x $y) $epsilon;
within $demo:epsilon 2 | + 2 (frac $demo:epsilon 2);
not | within $demo:epsilon 2 | + 2 (* $demo:epsilon 2);
define range | ? x:- | ? x:+ | if (<= $x:+ $x:-) (vector) | prepend $x:- | range (+ 1 $x:-) $x:+;
= 12 | reduce $+ | map (? x | * $x 2) | range 0 4;
define float | ? x:list | ? y | ? z | if (= 0 | list-length | $x:list) 0 | + (* $z | head $x:list) | float (tail $x:list) $y (* $y $z);
define decimal | ? x | ? x:list | + $x | float $x:list (frac 1 10) (frac 1 10);
within $demo:epsilon (frac 1 3) | decimal 0 | vector 3 3 3 3 3 3;
within $demo:epsilon (frac 9 7) | decimal 1 | vector 2 8 5 7 1 4;
define e:hat | reduce $+ | map (? x | frac 1 | factorial $x) | range 0 100;
within $demo:epsilon $e | decimal 2 | vector 7 1 8 2 8;
define pi:part | ? x | frac (if (even $x) (minus 1) 1) | * (* $x 2) | * (+ 1 | * $x 2) (+ 2 | * $x 2);
define pi:hat | + 3 | * 4 | reduce $+ | map $pi:part | range 1 100;
within $demo:epsilon $pi | decimal 3 | vector 1 4 1 5 9 2 6 5 3 5;
define power:10 | ? n | if (= $n 0) 1 | assign part (if (>= $n 0) 10 (frac 1 10)) | reduce $* | map (? x $part) | range 0 (abs $n);
define float:= | ? x | ? y | if (= $x $y) $true | within (frac (+ $x $y) 200000) $x $y;
float:= (frac 1 10) | power:10 | minus 1;
float:= (frac 1 100) | power:10 | minus 2;
define decimal:power | ? x:power | ? x:int | ? x:list | * (power:10 $x:power) (decimal $x:int $x:list);
float:= 1530 | decimal:power 3 1 | vector 5 3;
float:= 15300 | decimal:power 4 1 | vector 5 3;
float:= (decimal 1 | vector 5 3) | decimal:power 0 1 | vector 5 3;
float:= (decimal 0 | vector 0 0 1 5 3) | decimal:power (minus 3) 1 | vector 5 3;
define pow:int | ? x | ? n | if (= $n 0) 1 | assign part (if (>= $n 0) $x (frac 1 $x)) | reduce $* | map (? y $part) | range 0 (abs $n);
float:= (decimal 1 | vector 1 8 9 2 0) | pow 2 (decimal 0 | vector 2 5);
float:= (decimal 1 | vector 4 1 4 2 1) | pow 2 (decimal 0 | vector 5);
float:= (decimal 1 | vector 6 8 1 7 9) | pow 2 (decimal 0 | vector 7 5);
float:= (decimal 2 | vector 3 7 8 4 1) | pow 2 (decimal 1 | vector 2 5);
float:= (decimal 2 | vector 8 2 8 4 2) | pow 2 (decimal 1 | vector 5);
float:= (decimal 3 | vector 3 6 3 5 8) | pow 2 (decimal 1 | vector 7 5);
float:= (decimal 4 | vector 7 5 6 8 2) | pow 2 (decimal 2 | vector 2 5);
float:= (decimal 5 | vector 6 5 6 8 5) | pow 2 (decimal 2 | vector 5);
float:= (decimal 6 | vector 7 2 7 1 7) | pow 2 (decimal 2 | vector 7 5);
float:= (decimal 1 | vector 3 1 6 0 7) | pow 3 (decimal 0 | vector 2 5);
float:= (decimal 1 | vector 7 3 2 0 5) | pow 3 (decimal 0 | vector 5);
float:= (decimal 2 | vector 2 7 9 5 0) | pow 3 (decimal 0 | vector 7 5);
float:= (decimal 3 | vector 9 4 8 2 2) | pow 3 (decimal 1 | vector 2 5);
float:= (decimal 5 | vector 1 9 6 1 5) | pow 3 (decimal 1 | vector 5);
float:= (decimal 6 | vector 8 3 8 5 2) | pow 3 (decimal 1 | vector 7 5);
float:= (decimal 11 | vector 8 4 4 6 6) | pow 3 (decimal 2 | vector 2 5);
float:= (decimal 15 | vector 5 8 8 4 5) | pow 3 (decimal 2 | vector 5);
float:= (decimal 20 | vector 5 1 5 5 6) | pow 3 (decimal 2 | vector 7 5);
float:= (decimal 1 | vector 4 1 4 2 1) | pow 4 (decimal 0 | vector 2 5);
float:= 2 | pow 4 (decimal 0 | vector 5);
float:= (decimal 2 | vector 8 2 8 4 2) | pow 4 (decimal 0 | vector 7 5);
float:= (decimal 5 | vector 6 5 6 8 5) | pow 4 (decimal 1 | vector 2 5);
float:= 8 | pow 4 (decimal 1 | vector 5);
float:= (decimal 11 | vector 3 1 3 7 0) | pow 4 (decimal 1 | vector 7 5);
float:= (decimal 22 | vector 6 2 7 4 1) | pow 4 (decimal 2 | vector 2 5);
float:= 32 | pow 4 (decimal 2 | vector 5);
float:= (decimal 45 | vector 2 5 4 8 3) | pow 4 (decimal 2 | vector 7 5);
define exp:hat | ? x | reduce $+ | map (? n | frac (pow:int $x $n) | factorial $n) | range 0 50;
define ln:10:hat | decimal 2 | vector 3 0 2 5 8 5 0 9 2 9 9;
float:= (pow:int 10 2) (exp:hat | * 2 $ln:10:hat);
float:= (pow:int 10 3) (exp:hat | * 3 $ln:10:hat);
float:= (pow:int 10 4) (exp:hat | * 4 $ln:10:hat);
21. introduce i
A very very abbreviated introduction of complex numbers
define all-equal | ? x:list | if (>= 1 | list-length $x:list) $true | and (= (list-ref $x:list 0) (list-ref $x:list 1)) (all-equal | tail $x:list);
define complex | ? x | ? y | + $x | * $y $i;
= (complex 5 6) | + (complex 3 2) (complex 2 4);
= (complex 7 22) | * (complex 5 4) (complex 3 2);
= (complex 10 8) | * (complex 5 4) 2;
= (complex 10 8) | * 2 (complex 5 4);
should work through how to divide complex numbers (multiply by conjugate)
= (complex (frac 6 25) (frac 17 25)) | frac (complex 3 2) (complex 4 | minus 3);
all-equal | vector (+ 7 | * 22 $i) (* (+ 5 | * 4 $i) (+ 3 | * 2 $i)) (sum | vector (* 5 3) (* 5 (* 2 $i)) (* (* 4 $i) 3) (* (* 4 $i) (* 2 $i))) (sum | vector 15 (* 10 $i) (* 12 $i) (minus 8)) (sum | vector (+ 15 (minus 8)) (* (+ 10 12) $i));
Hint at Euler’s identity
float:= 0 | + 1 | exp:hat | * $pi $i;
22. define let expressions
Sometimes it is nice to do a lot of assignments at once.
We introduce let ((k1 v1) (k2 v2)) body which is equivalent to
assign k1 v1 | assign k2 v2 | body.
define translate:let | ? x | ? y | if (= 0 | list-length $x) (translate $y) | translate:let (tail $x) | vector assign (head | head $x) (head | tail | head $x) $y;
define translate | ? x | if (not | function? $x) (translate:let:begin $x) | if (not | = let | head $x) (translate:let:begin $x) | translate:let (head | tail $x) (head | tail | tail $x);
let ((x 50) (y 20)) | = 30 | - $x $y;
= (let ((x 10)) | + $x 5) (assign x 10 | + $x 5);
= (let ((x 10)) | + $x 5) ((? x | + $x 5) 10);
= (let ((x 10) (y 5)) | + $x $y) (assign x 10 | assign y 5 | + $x $y);
= (let ((x 10) (y 5)) | + $x $y) ((? x | ? y | + $x $y) 10 5);
23. lambda functions
define translate | let ((x:translate $translate:lambda:begin)) | ? x | if (not | function? $x) (x:translate $x) | if (not | = lambda | head $x) (x:translate $x) | let ((x:list | head | tail $x) (y | head | tail | tail $x)) | if (= 0 | list-length $x:list) (translate $y) | translate | vector lambda (except-last $x:list) | vector ? (last $x:list) $y;
= 8 | (lambda (x y) | - $x $y) 8 0;
= 2 | (lambda (x y) | - $x $y) 4 2;
= 3 | (lambda (x y) | - $x $y) 9 6;
= 3 | (lambda (x y) | - $x $y) 4 1;
= 0 | (lambda (x y) | - $x $y) 4 4;
24. end of part 1, start of part 2
# The following parts of the message are experimental, and not # carefully integrated with the main body
25. some pure lambda calculus definitions - optional
# these definitions are not quite what we want # since thinking of everything as a function requires headscratching # it would be better to use these as a parallel means of evaluation # ... for expressions
define pure:if | ? x | ? y | ? z | x $y $z;
define pure:cons | ? x | ? y | ? z | pure:if $z $x $y;
define pure:2 | ? y | ? x | y (y $x);
define pure:next | ? n | ? y | ? x | y ((n $y) $x);
define pure:+ | ? x | ? y | (x $pure:next) $y;
define pure:* | ? x | ? y | (x (pure:+ $y)) $pure:0;
define pure:prev | ? x:pure | pure:cdr | (x:pure (? x:? | pure:cons (pure:next | pure:car $x:?) (pure:car $x:?))) (pure:cons $pure:0 $pure:0);
define pure:=:0 | ? x:pure | (x:pure (? y $pure:false) $pure:true);
define fixed-point | ? x | (? y | x (y $y)) (? y | x (y $y));
# .. but for rest of message will assume that define does fixed-point for us # now build a link between numbers and church number functions
define pure:int:get | ? y | y (? x | + $x 1) 0;
define int:pure:get | ? x | if (= 0 $x) $pure:0 (pure:next | int:pure:get | - $x 1);
26. introduce universal quantifier
# really need to link with sets for true correctness # and the examples here are REALLY sparse, need much more
not | forall (? x | < $x (* $x 2));
27. introduce existential quantifier
# really need to link with sets for true correctness # and the examples here are REALLY sparse, need much more
not (exists (? x | = $x (+ $x 2)));
28. introduce logical implication
define => | ? x | ? y | not | and $x (not $y);
forall (? x | forall (? y | => (=> $x $y) (=> (not $y) (not $x))));
29. introduce sets and set membership
define element | ? x | ? y:list | not | = $undefined | list:find $y:list $x;
Set some rules for set equality.
define set:<= | ? x | ? y | if (= 0 | list-length $x) $true | and (element (head $x) $y) | set:<= (tail $x) $y;
define set:= | ? x | ? y | and (set:<= $x $y) (set:<= $y $x);
set:= (vector 1 5 9) (vector 5 1 9);
set:= (vector 1 5 9) (vector 9 1 5);
not | set:= (vector 1 5 9) (vector 1 5);
let’s go leave ourselves wide open to Russell’s paradox by using characteristic functions since it doesn’t really matter within the bounds of this message
element 5 | all | ? x | = 15 | + $x 10;
element 3 | all | ? x | = (* $x 3) (+ $x 6);
forall | ? x | => (element $x $set:int:+) (element (+ $x 1) $set:int:+);
define set:true:false | vector $true $false;
define set:even | all | ? x | exists | ? y | and (element $y $set:int:+) (= $x | * 2 $y);
30. introduce graph structures
define graph:make | lambda (x:graph:1 x:graph:2) | pair $x:graph:1 $x:graph:2;
define demo:graph | graph:make (vector 1 2 3 4) (vector (pair 1 2) (pair 2 3) (pair 1 4));
define exists:graph:2 | lambda (x:graph y:graph:1 z:graph:1) | exists | ? n | if (or (< $n 0) (>= $n | list-length | list-ref $x:graph 1)) $false | list= (list-ref (list-ref $x:graph 1) $n) (pair $y:graph:1 $z:graph:1);
define exists:graph:2:list | lambda (x:graph y:graph:1 z:graph:1) | if (= $y:graph:1 $z:graph:1) $true | if (exists:graph:2 $x:graph $y:graph:1 $z:graph:1) $true | exists | ? n:graph:1 | if (not | exists:graph:2 $x:graph $y:graph:1 $n:graph:1) $false | exists:graph:2:list $x:graph $n:graph:1 $z:graph:1;
not | exists:graph:2:list $demo:graph 2 4;
31. show how to execute a sequence of instructions
define translate | let ((prev $translate:begin:prev)) | ? x | if (not | function? $x) (prev $x) | if (not | = (head $x) begin) (prev $x) | translate | vector (vector ? x (vector last (vector x))) (prepend vector | tail $x);
= 6 | begin (set! $demo:make-cell:x 88) (set! $demo:make-cell:x 6) (get! $demo:make-cell:x);
= 88 | begin (set! $demo:make-cell:y 88) (set! $demo:make-cell:x 6) (get! $demo:make-cell:y);
= 4 | begin (set! $demo:make-cell:x 88) (set! $demo:make-cell:x 6) (get! $demo:make-cell:x) 4;
32. introduce environment/hashmap structure
# this section needs a LOT more examples :-) # note that at the time of writing (h 1 2) is same as ((h) 1 2)
define hash-add | lambda (x:hash x y z) (if (equal $z $x) $y (x:hash $z));
define hash-ref | lambda (x:hash x) (x:hash $x);
define hash-default | ? default | ? x $default;
define demo:hash | hash-add (hash-add $hash-null 3 2) 4 9;
= (hash-ref (hash-add $demo:hash 15 33) 15) 33;
define make-hash | ? x | if (list= $x (vector)) $hash-null (hash-add (make-hash (tail $x)) (first | head $x) (second | head $x));
= (hash-ref (make-hash | vector (pair 3 10) (pair 2 20) (pair 1 30)) 3) 10;
= (hash-ref (make-hash | vector (pair 3 10) (pair 2 20) (pair 1 30)) 1) 30;
33. introduce simple mutable structures
define mutable-struct | ? x:list | let ((cell:list | map (? x | make-cell 0) $x:list)) | ? x:find | list-ref $cell:list | list:find $x:list $x:find;
define demo:mutable-struct | mutable-struct | vector x:1 x:2 x:3;
34. introduce turing machine model
This is just for fun, as an exercise.
define tape:tail | ? x | if (>= 1 | list-length $x) (vector | vector) | tail $x;
define tape:head | ? x | if (= 0 | list-length $x) (vector) | head $x;
define tape:get | ? tape | tape:head | second $tape;
define tape:next | lambda (tape n x) | if (= $n 1) (pair (prepend $x | first $tape) (tape:tail | second $tape)) | if (= $n 0) (pair (tape:tail | first $tape) (prepend (tape:head | first $tape) (prepend $x (tape:tail | second $tape)))) | pair (first $tape) (prepend $x (tape:tail | second $tape));
define tape:do | lambda (x:function current end tape) | if (= $current $end) $tape | let ((next | x:function $current | tape:get $tape)) | tape:do $x:function (list-ref $next 0) $end | tape:next $tape (list-ref $next 1) (list-ref $next 2);
define tape:make | ? x | pair (vector) $x;
define tape:-:tail | ? x | ? x:list | if (= 0 | list-length $x:list) $x:list | if (not | equal $x | last $x:list) $x:list | tape:-:tail $x (except-last $x:list);
define tape:result | ? x | tape:-:tail (vector) (second $x);
define demo:tape:function:+:1 | make-hash | vector (pair next (make-hash | vector (pair 0 (vector next 1 0)) (pair 1 (vector next 1 1)) (pair (vector) (vector +:1 0 (vector))))) (pair +:1 (make-hash | vector (pair 0 (vector not:+:1 0 1)) (pair 1 (vector +:1 0 0)) (pair (vector) (vector end 2 1)))) (pair not:+:1 (make-hash | vector (pair 0 (vector not:+:1 0 0)) (pair 1 (vector not:+:1 0 1)) (pair (vector) (vector end 1 (vector))))) (pair end (make-hash | vector));
list= (vector 1 0 1 0) | tape:result | tape:do $demo:tape:function:+:1 next end (tape:make | vector 1 0 0 1);
list= (vector 1 0 0 0) | tape:result | tape:do $demo:tape:function:+:1 next end (tape:make | vector 1 1 1);
list= (vector 1 1 1 0 0 1 0 0 0) | tape:result | tape:do $demo:tape:function:+:1 next end (tape:make | vector 1 1 1 0 0 0 1 1 1);
35. quoting syntax
define quote-f | ? key | ? x | if (not | function? $x) $x | if (= $key | list-ref $x 0) (tail $x) | prepend vector | map (quote-f $key) $x;
list= (quote-f x | vector 1) | vector vector 1;
list= (quote-f x | vector 1 2 3) | vector vector 1 2 3;
list= (quote-f x | vector 1 (vector 5 2) 3) | vector vector 1 (vector vector 5 2) 3;
list= (quote-f x | vector 1 (vector 5 2) (vector x + 5 2)) | vector vector 1 (vector vector 5 2) (vector + 5 2);
define translate | assign prev $translate | ? x | if (not | function? $x) $x | if (not | = quote | head $x) (prev $x) | translate | quote-f (list-ref $x 1) (list-ref $x 2);
list= (quote x | 1 2 3) | vector 1 2 3;
list= (quote x | 1 (5 2) 3) | vector 1 (vector 5 2) 3;
list= (quote x | 1 (5 2) (x + 5 2)) | vector 1 (vector 5 2) 7;
36. introduce simple form of typing, for ease of documentation.
An object is simply a function that takes an argument. The argument is the method to call on the object. Types are here taken to be just the existence of a particular method, with that method returning an object of the appropriate type.
define make-integer | ? x | ? n | if (= $n int) $x 0;
define objectify | ? x | if (function? $x) $x | make-integer $x;
add version of lambda that allows types to be declared
define translate | let ((prev $translate)) | ? x | if (not | function? $x) (prev $x) | if (not | = lambda | head $x) (prev $x) | let ((formals | head | tail $x) (body | head | tail | tail $x)) | if (= 0 | list-length $formals) (translate $body) | if (not | function? | last $formals) (translate | vector lambda (except-last $formals) (vector ? (last $formals) $body)) | let ((formal-name | first | last $formals) (formal-type | second | last $formals)) | translate | vector lambda (except-last $formals) | vector ? $formal-name | vector let (vector (vector $formal-name (vector (vector objectify | vector $formal-name) $formal-type))) $body;
add conditional form
define translate | let ((prev $translate)) | ? x | if (not | function? $x) (prev $x) | if (not | = cond | head $x) (prev $x) | let ((cnd | head | tail $x) (rem | tail | tail $x)) | if (= 0 | list-length $rem) (translate $cnd) | translate (vector if (first $cnd) (second $cnd) (prepend cond $rem));
= 7 | cond ($false 3) ($true 7) 11;
= 3 | cond ($true 3) ($true 7) 11;
= 11 | cond ($false 3) ($false 7) 11;
define remove-match | lambda (test lst) | if (= 0 | list-length $lst) $lst | if (test | head $lst) (remove-match $test (tail $lst)) | prepend (head $lst) (remove-match $test (tail $lst));
define remove-element | ? x | remove-match (? y | = $y $x);
list= (vector 1 2 3 5) | remove-element 4 | vector 1 2 3 4 5;
list= (vector 1 2 3 5) | remove-element 4 | vector 1 4 2 4 3 4 5;
define instanceof | ? T | ? t | if (not | function? $t) (= $T int) | function? | (objectify $t) $T;
define return | ? T | ? t | let ((obj | objectify $t)) | obj $T;
define tester | lambda ((x int) (y int)) | return int | + $x $y;
= 42 | tester (make-integer 10) (make-integer 32);
define reflective | ? f | (? x | f | ? y | (x $x) $y) (? x | f | ? y | (x $x) $y);
define woop | reflective | ? self | ? x | if (= $x 10) 22 (self 10);
37. message passing / object example - a 2D point
define point | lambda (x y) | reflective | lambda (self msg) | cond ((= $msg x) $x) ((= $msg y) $y) ((= $msg point) $self) ((= $msg +) | lambda ((p point)) | point (+ $x | p x) (+ $y | p y)) ((= $msg =) | lambda ((p point)) | and (= $x | p x) (= $y | p y)) 0;
(point 100 200) + (point 200 100) = (point 300 300);
38. message passing / object example - a container
define container | ? x | assign contents (make-cell | vector) | reflective | lambda (self msg) | cond ((= $msg container) $self) ((= $msg inventory) | get! $contents) ((= $msg add) | ? x | if (element $x | get! $contents) $false | set! $contents | prepend $x | get! $contents) ((= $msg remove) | ? x | set! $contents | remove-element $x | get! $contents) ((= $msg =) | lambda ((c container)) | set:= (self inventory) (c inventory)) 0;
set:= (pocket inventory) | vector 77 88 99;
set:= (pocket inventory) | vector 77 99;
a sketch of inheritance - add one method to container (count)
define counter-container | ? x | assign super (container new) | reflective | lambda (self msg) | cond ((= $msg counter-container) $self) ((= $msg count) | list-length | super inventory) (super $msg);
39. adding a special form for classes
define list-append | lambda (lst1 lst2) | if (= 0 | list-length $lst1) $lst2 | list-append (except-last $lst1) | prepend (last | $lst1) $lst2;
list= (vector 1 2 3 4 5 6) | list-append (vector 1 2 3) (vector 4 5 6);
define unique | assign store (make-cell 0) | ? x | assign id (get! $store) | begin (set! $store (+ $id 1)) $id;
define setup-this | lambda (this self) | if (function? $this) $this $self;
define standard-class-methods | ? name | quote @@ | ((= $method self) $self) ((= $method (@@ name)) (self self)) ((= $method classname) (@@ name)) ((= $method unknown) | ? x 0) ((= $method new) 0) ((= $method unique-id) $unique-id) ((= $method ==) | ? x | = $unique-id | x unique-id) (self unknown $method);
define custom-class-methods | lambda (name args fields) | list-append (map (? x | quote @@ | (= $method | @@ first $x) (@@ second $x)) (map $tail | select-match (? x | = method | first $x) $fields)) (map (? x | quote @@ | (= $method | @@ x) ((@@ x))) (map $second | select-match (? x | = field | first $x) $fields));
define class-cond | lambda (name args fields) | prepend cond | list-append (custom-class-methods $name $args $fields) (standard-class-methods $name);
define translate | assign prev $translate | ? x | if (not | function? $x) (prev $x) | if (not | = class | head $x) (prev $x) | let ((name | list-ref $x 1) (args | list-ref $x 2) (fields | tail | tail | tail $x)) | translate | quote @@ | define (@@ name) | lambda (@@ prepend ext-this $args) | let (@@ append (vector unique-id | vector unique new) (map $tail | select-match (? x | = field | first $x) $fields)) | let ((self | reflective | lambda (self) | let ((this | setup-this $ext-this $self)) | lambda (method) | @@ class-cond $name $args $fields)) | begin (self new) $self;
class point (x y) (method x $x) (method y $y) (method + | lambda ((p point)) | point new (+ $x | p x) (+ $y | p y)) (method = | lambda ((p point)) | and (= $x | p x) (= $y | p y));
= 11 | ((point new 11 12) point) x;
= 16 | ((point new 16 17) point) x;
point1 + $point2 = | point new 3 33;
point2 + $point1 = | point new 3 33;
(point new 100 200) + (point new 200 100) = (point new 300 300);
40. wrapper class for cells
class cell (initial-value) (field content | make-cell $initial-value) (method get | get! $content) (method set | ? new-value | set! $content $new-value) (method reset | self set $initial-value) (method unknown | ? x | (objectify | self get) $x);
define cell-test2 | cell new | point new 120 150;
define cell-test3 | cell new | point new 300 300;
cell-test2 + $cell-test3 = | point new 420 450;
41. playing around with doors and rooms
class door ((src room) (dest room)) (method new | begin (src add $self) (dest add $self)) (method access-from | lambda ((current room)) | cond ((current == $src) $dest) ((current == $dest) $src) 0) (method is-present | lambda ((current room)) | or (current == $src) (current == $dest));
class room (name) (field content | container new) (method name $name) (method unknown | ? x | content $x);
need to fix up containers to use object equality
define object-element | lambda (n lst) | < 0 | list-length | select-match (? x | x == $n) $lst;
class container () (field contents | cell new (vector)) (method inventory | contents get) (method add | ? x | if (object-element $x | contents get) $false | contents set | prepend $x | contents get);
define door1 | door new $hall $kitchen;
(first | kitchen inventory) == $door1;
(door1 access-from $hall) == $kitchen;
(door1 access-from $kitchen) == $hall;
define door3 | door new $hall $stairs;
define door4 | door new $stairs $bedroom;
class character () (field location | cell new 0) (field name | cell new 0) (method set-room | lambda ((r room)) | begin (if (not | function? | location get) 0 | location get remove $self) (r add $self) (location set $r)) (method get-room | location get) (method set-name | ? n | name set $n) (method get-name | name get) (method update 0);
define find-max-helper | lambda (test max idx n lst) | if (= 0 | list-length $lst) $idx | if (> (test | head $lst) $max) (find-max-helper $test (test | head $lst) $n (+ $n 1) (tail $lst)) (find-max-helper $test $max $idx (+ $n 1) (tail $lst));
define find-max-idx | lambda (test lst) | find-max-helper $test (test | head $lst) 0 0 $lst;
define find-min-helper | lambda (test max idx n lst) | if (= 0 | list-length $lst) $idx | if (< (test | head $lst) $max) (find-min-helper $test (test | head $lst) $n (+ $n 1) (tail $lst)) (find-min-helper $test $max $idx (+ $n 1) (tail $lst));
define find-min-idx | lambda (test lst) | find-min-helper $test (test | head $lst) 0 0 $lst;
= 2 | find-max-idx (? x $x) | vector 3 4 5 0;
= 1 | find-max-idx (? x $x) | vector 3 5 4 0;
= 0 | find-max-idx (? x $x) | vector 5 3 4 0;
= 2 | find-min-idx (? x $x) | vector 3 4 0 2;
= 1 | find-min-idx (? x $x) | vector 3 1 4 2;
= 0 | find-min-idx (? x $x) | vector 1 3 4 2;
the ‘robo’ class makes a character that patrols from room to room
class robo () (field super | character new) (field timestamp | cell new 1) (field timestamp-map | cell new (? x 0)) (method unknown | ? x | super $x) (method update | assign exits (select-match (? x | instanceof door $x) (self location inventory)) | assign timestamps (map (? x | timestamp-map get $x) $exits) | assign chosen-exit (list-ref $exits | find-min-idx (? x $x) $timestamps) | assign current-tmap (timestamp-map get) | assign current-t (timestamp get) | begin (self location set | chosen-exit access-from | self location get) (timestamp-map set | lambda ((d door)) | if (d == $chosen-exit) $current-t (current-tmap $d)) (timestamp set | + 1 | timestamp get));
define which-room | lambda ((rr robo)) | find-max-idx (lambda ((r room)) | if (r == | rr get-room) 1 0) | vector $hall $kitchen $stairs $lawn $bedroom;
define sequencer | lambda (n current lst) | if (>= $current $n) $lst | begin (myrobo update) (sequencer $n (+ $current 1) (append (which-room $myrobo) $lst));
here is a list of the first 30 rooms the robot character visits 0=hall, 1=kitchen, 2=stairs, 3=lawn, 4=bedroom
list= (sequencer 30 0 (vector)) | vector 4 2 0 3 0 1 0 2 4 2 0 3 0 1 0 2 4 2 0 3 0 1 0 2 4 2 0 3 0 1;
Now should start to introduce a language to talk about what is going on in the simulated world, and start to move away from detailed mechanism
42. introduce the elements
Introducing the elements is done well in the DearET message by Michael Busch. We draw inspiration from that work.
The general idea here is that there are some physical ratios that should be known by anybody with a handle on what is going on at the atomic level, and may be recognizable. The pattern of how elementary particles are combined into atoms, and atoms into molecules, may also ring a bell.
The following definitions are not included in the message, since they are unit-specific. The message will only present ratios.
assume | define proton | make-hash | vector (pair mass | decimal:power (minus 27) 1 | vector 6 7 2 6 1 9 2 3 6 9) (pair charge 1);
assume | define electron | make-hash | vector (pair mass | decimal:power (minus 31) 9 | vector 1 0 9 3 8 3 5 6) (pair charge | minus 1);
assume | define neutron | make-hash | vector (pair mass | decimal:power (minus 27) 1 | vector 6 7 4 9 2 7 4 7 1) (pair charge 0);
float:= (proton mass) | * (electron mass) | decimal 1836 | vector 1 5 2 6 7 3;
float:= (electron mass) | * (proton mass) | decimal 0 | vector 0 0 0 5 4 4 6 1 7;
float:= (neutron mass) | * (proton mass) | decimal 1 | vector 0 0 1 3 7 8 4 2;
float:= (proton charge) | * (electron charge) (minus 1);
define atom | ? x:proton | ? x:proton:neutron | make-hash | vector (pair proton $x:proton) (pair neutron | - $x:proton:neutron $x:proton) (pair electron $x:proton);
class elemental (proton isotope:list) (method proton $proton) (method isotope:list $isotope:list) (method electron $proton) (method neutron:list | map (? x | - $x $proton) $isotope:list);
define hydrogen | elemental new 1 | vector 1 2;
define helium | elemental new 2 | vector 2 4;
define carbon | elemental new 6 | vector 12 13;
define nitrogen | elemental new 7 | vector 14 15;
define oxygen | elemental new 16 | vector 16 17 18;
list= (hydrogen isotope:list) | vector 1 2;
list= (hydrogen neutron:list) | vector 0 1;
list= (carbon isotope:list) | vector 12 13;
list= (carbon neutron:list) | vector 6 7;
class molecule (elemental:list) (method elemental:list $elemental:list) (method count | lambda ((e elemental)) | list-length | select-match (? x | = (x proton) (e proton)) $elemental:list);
define hydrogen:2 | molecule new | vector $hydrogen $hydrogen;
define oxygen:2 | molecule new | vector $oxygen $oxygen;
define oxygen:3 | molecule new | vector $oxygen $oxygen $oxygen;
define water | molecule new | vector $hydrogen $hydrogen $oxygen;
define nitrogen:2 | molecule new | vector $nitrogen $nitrogen;
define ammonia | molecule new | vector $nitrogen $hydrogen $hydrogen $hydrogen;
define methane | molecule new | vector $carbon $hydrogen $hydrogen $hydrogen $hydrogen;
define ethane | molecule new | vector $hydrogen $hydrogen $hydrogen $carbon $carbon $hydrogen $hydrogen $hydrogen;
43. end of part 2, start of part 3
# The following parts of the message are the beginnings # of embedding an alternate visual primer
44. simulating unless gates
# for embedded image-and-logic-based primer
# practice with pure logic gate
# X unless Y = (X if Y=0, otherwise 0)
define unless | ? x | ? y | and $x | not $y;
# if second input is true, output is blocked (false) # if second input is false, output copies first input
# To do: add a simple simulator for non-grid-based # logic -- much simpler to understand than # grid-based
# On to a grid-based logic simulation # first, need unbounded, mutable matrices
define make-matrix | ? default | make-cell | hash-default $default;
define matrix-set | ? m | ? x | ? addr | set! $m | hash-add (get! $m) $addr $x;
define matrix-get | ? m | ? addr | hash-ref (get! $m) $addr;
= 0 | matrix-get $test-matrix | vector 1 2 3;
matrix-set $test-matrix 10 | vector 1 2 3;
= 10 | matrix-get $test-matrix | vector 1 2 3;
# go through a circuit of unless gates and analyze data flow
define unless-phase-1 | ? circuit | assign state (make-matrix $false) | begin (map (? gate | assign x1 (list-ref $gate 0) | assign y1 (list-ref $gate 1) | assign x2 (list-ref $gate 2) | assign y2 (list-ref $gate 3) | assign v (list-ref $gate 4) | (if (= $x1 $x2) (begin (matrix-set $state $v | vector $x2 $y2 vert-value) (matrix-set $state $true | vector $x2 $y2 vert-have) (matrix-set $state $true | vector $x1 $y1 vert-want) $gate) (begin (matrix-set $state $v | vector $x2 $y2 horiz-value) (matrix-set $state $true | vector $x2 $y2 horiz-have) (matrix-set $state $true | vector $x1 $y1 horiz-want) $gate))) $circuit) $state;
# move forward one simulation step
define unless-phase-2 | ? circuit | ? state | map (? gate | assign x1 (list-ref $gate 0) | assign y1 (list-ref $gate 1) | assign x2 (list-ref $gate 2) | assign y2 (list-ref $gate 3) | assign v (list-ref $gate 4) | assign nv (if (= $x1 $x2) (if (matrix-get $state | vector $x1 $y1 vert-have) (and (matrix-get $state | vector $x1 $y1 vert-value) (not | and (matrix-get $state | vector $x1 $y1 horiz-value) (not | matrix-get $state | vector $x1 $y1 horiz-want))) (if (matrix-get $state | vector $x1 $y1 horiz-have) (matrix-get $state | vector $x1 $y1 horiz-value) $true)) (if (matrix-get $state | vector $x1 $y1 horiz-have) (and (matrix-get $state | vector $x1 $y1 horiz-value) (not | and (matrix-get $state | vector $x1 $y1 vert-value) (not | matrix-get $state | vector $x1 $y1 vert-want))) (if (matrix-get $state | vector $x1 $y1 vert-have) (matrix-get $state | vector $x1 $y1 vert-value) $true))) | vector $x1 $y1 $x2 $y2 $nv) $circuit;
# wrap up both phases of simulation
define simulate-unless | ? circuit | assign state (unless-phase-1 $circuit) | unless-phase-2 $circuit $state;
# A circuit is a list of gates # Each gate is a list (x1 y1 x2 y2 v) # where the coordinates (x1,y1) and (x2,y2) represent # start and end points of a wire on a plane, carrying a # logic value v. # Wires copy values from their start point. # | # | (A) # V # -->--> # (B)(C) # # Wire C here copies from wire B. # If wire A is on, it blocks (sets to 0) C.
assign circuit1 (vector (vector 2 2 4 2 $true) (vector 4 2 6 2 $true) (vector 6 2 8 2 $true) (vector 6 4 6 2 $true)) | assign circuit2 (vector (vector 2 2 4 2 $true) (vector 4 2 6 2 $true) (vector 6 2 8 2 $false) (vector 6 4 6 2 $true)) | equal (simulate-unless $circuit1) $circuit2;
# okay, now let us make a simple image class # we are going to encode each row as a single binary number, # rather than a vector, so that images will be pretty # obvious in the raw, uninterpreted message # TODO: introduce div somewhere!
define bit-get | lambda (n offset) | assign div2 (div $n 2) | if (= 0 | offset) (not | = $n | * 2 $div2) | bit-get $div2 | - $offset 1;
= 0 | bit-get (::::::::::::::......:...:..::.) 0;
= 1 | bit-get (::::::::::::::......:...:..::.) 1;
= 1 | bit-get (::::::::::::::......:...:..::.) 2;
= 0 | bit-get (::::::::::::::......:...:..::.) 3;
= 0 | bit-get (::::::::::::::......:...:..::.) 4;
= 1 | bit-get (::::::::::::::......:...:..::.) 5;
= 0 | bit-get (::::::::::::::......:...:..::.) 6;
= 0 | bit-get (::::::::::::::......:...:..::.) 7;
= 0 | bit-get (::::::::::::::......:...:..::.) 8;
= 1 | bit-get (::::::::::::::......:...:..::.) 9;
define make-image | lambda (h w lst) | vector $h $w $lst;
define image-get | lambda (image row col) | assign h (list-ref $image 0) | assign w (list-ref $image 1) | assign lst (list-ref $image 2) | assign bits (list-ref $lst $row) | bit-get $bits | - (- $w $col) 1;
define image-height | ? image | list-ref $image 0;
define image-width | ? image | list-ref $image 1;
define test-image | make-image 3 20 | vector (:...................) (:...:...............) (:...................);
# need a way to join two lists # TODO: is this similar to "list-append" in NewType?
define merge-list | ? lst1 | ? lst2 | if (= 0 | list-length $lst1) $lst2 | prepend (head $lst1) | merge-list (tail $lst1) $lst2;
define merge-lists | ? lst | if (> (list-length $lst) 2) (merge-list (head $lst) (merge-lists | tail $lst)) (if (= (list-length $lst) 2) (merge-list (head $lst) | (head | tail $lst)) (if (= (list-length $lst) 1) (head $lst) (vector)));
equal (vector 1 2 3 4) | merge-list (vector 1 2) (vector 3 4);
equal (vector 1 2 3 4) | merge-lists (vector (vector 1 2) (vector 3) (vector 4));
# helper for pairing
define prefix | ? x | ? lst | map (? y (vector (x) (y))) $lst;
equal (vector (vector 1 10) (vector 1 11)) (prefix 1 | vector 10 11);
# need a way to take product of domains
define pairing | ? lst1 | ? lst2 | if (= 0 | list-length $lst1) (vector) | merge-list (prefix (head $lst1) $lst2) (pairing (tail $lst1) $lst2);
equal (vector (vector 1 10) (vector 1 11) (vector 2 10) (vector 2 11)) | pairing (vector 1 2) (vector 10 11);
# need a way to make counting sets # TODO: is this like range?
define count | ? lo | ? hi | if (> $lo $hi) (vector) | prepend $lo | count (+ $lo 1) $hi;
equal (vector 0 1 2 3 4) (count 0 4);
# given an image of a circuit, extract a model. # wire elements are centered on multiples of 8
# individual element...
define distill-element | ? image | ? xlogic | ? ylogic | ? xmid | ? ymid | if (not | image-get $image $ymid $xmid) (vector) | assign vert (image-get $image (+ $ymid 4) $xmid) | assign dx (if $vert 0 1) | assign dy (if $vert 1 0) | assign pos (image-get $image (+ $ymid | + (* 4 $dy) (* 2 $dx)) (+ $xmid | - (* 4 $dx) (* 2 $dy))) | assign sgn (if $pos 1 (minus 1)) | assign dx (* $sgn $dx) | assign dy (* $sgn $dy) | assign active (image-get $image (+ $ymid $dx) (- $xmid $dy)) | vector | vector (- $xlogic $dx) (- $ylogic $dy) (+ $xlogic $dx) (+ $ylogic $dy) $active;
# full circuit...
define distill-circuit | ? image | assign h (div (image-height $image) 8) | assign w (div (image-width $image) 8) | merge-lists | map (? v | assign xlogic (list-ref $v 0) | assign ylogic (list-ref $v 1) | assign xmid (* 8 $xlogic) | assign ymid (* 8 $ylogic) | distill-element $image $xlogic $ylogic $xmid $ymid) (pairing (count 1 (- $w 1)) (count 1 (- $h 1)));
45. testing alternate primer based on gates: cos_not circuit
# This section contains one or more representations of a circuit # constructed using UNLESS gates.
define cos_not_gate | vector (vector 0 6 2 6 $true) (vector 2 6 4 6 $true) (vector 4 6 6 6 $true) (vector 6 6 8 6 $true) (vector 8 4 8 6 $true) (vector 8 6 8 8 $false) (vector 8 8 10 8 $false) (vector 10 8 12 8 $false) (vector 12 8 12 6 $false) (vector 12 6 14 6 $false) (vector 14 6 16 6 $false) (vector 16 6 18 6 $false) (vector 18 6 20 6 $false);
define cos_not_image | make-image 109 169 | vector (:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:..............................................................:::......................................................................................................:) (:..............................................................:::......................................................................................................:) (:..............................................................:::......................................................................................................:) (:..............................................................:::......................................................................................................:) (:..............................................................:::......................................................................................................:) (:..............................................................:::......................................................................................................:) (:..............................................................:::......................................................................................................:) (:..............................................................:::......................................................................................................:) (:..............................................................:::......................................................................................................:) (:.............................................................:::::.....................................................................................................:) (:..............................................................:::......................................................................................................:) (:...........:...............:...............:...............:...:...........................................:...............:...............:...............:...........:) (:..:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..............................................::..............::..............::..............::..........:) (:..::::::::::::....::::::::::::....::::::::::::....::::::::::::....................................::::::::::::....::::::::::::....::::::::::::....::::::::::::.........:) (:..:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..............................................::..............::..............::..............::..........:) (:...........:...............:...............:...............:...................................:...........:...............:...............:...............:...........:) (:...............................................................:..............................:::......................................................................:) (:...............................................................:.............................:::::.....................................................................:) (:...............................................................:...............................:.......................................................................:) (:...............................................................:...............................:.......................................................................:) (:...............................................................:...............................:.......................................................................:) (:...............................................................:...............................:.......................................................................:) (:...............................................................:...............................:.......................................................................:) (:...............................................................:...............................:.......................................................................:) (:...............................................................:...............................:.......................................................................:) (:.............................................................:::::.............................:.......................................................................:) (:..............................................................:::..............................:.......................................................................:) (:...............................................................:...........:...............:...........................................................................:) (:...........................................................................::..............::..........................................................................:) (:..................................................................::::::::::::....::::::::::::.........................................................................:) (:...........................................................................::..............::..........................................................................:) (:...........................................................................:...............:...........................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::);
equal $cos_not_gate | distill-circuit $cos_not_image;
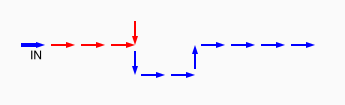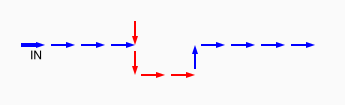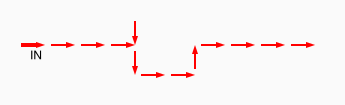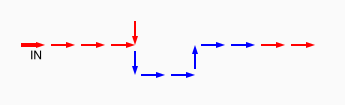
Run simulator
46. testing alternate primer based on gates: cos_and circuit
# This section contains one or more representations of a circuit # constructed using UNLESS gates.
define cos_and_gate | vector (vector 0 2 2 2 $true) (vector 0 8 2 8 $true) (vector 2 2 4 2 $true) (vector 2 4 4 4 $true) (vector 2 6 4 6 $true) (vector 2 8 4 8 $true) (vector 4 2 4 4 $true) (vector 4 8 4 6 $true) (vector 4 4 6 4 $false) (vector 4 6 6 6 $false) (vector 6 4 8 4 $false) (vector 6 6 8 6 $false) (vector 8 4 10 4 $false) (vector 8 6 10 6 $false) (vector 10 2 10 4 $true) (vector 10 4 10 6 $true) (vector 10 6 10 8 $true) (vector 10 8 12 8 $true) (vector 12 8 14 8 $true) (vector 14 8 16 8 $true) (vector 16 8 18 8 $true);
define cos_and_image | make-image 88 153 | vector (:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::) (:.......................................................................................................................................................:) (:.......................................................................................................................................................:) (:.......................................................................................................................................................:) (:.......................................................................................................................................................:) (:.......................................................................................................................................................:) (:.......................................................................................................................................................:) (:.......................................................................................................................................................:) (:.......................................................................................................................................................:) (:.......................................................................................................................................................:) (:.......................................................................................................................................................:) (:.......................................................................................................................................................:) (:.......................................................................................................................................................:) (:.......................................................................................................................................................:) (:...........:...............:...........................................................................................................................:) (:..:::::::::::.....:::::::::::..........................................................................................................................:) (:..::::::::::::....::::::::::::.........................................................................................................................:) (:..:::::::::::.....:::::::::::..........................................................................................................................:) (:...........:...............:...........................................................................................................................:) (:..............................:::.............................................:::......................................................................:) (:..............................:::.............................................:::......................................................................:) (:..............................:::.............................................:::......................................................................:) (:..............................:::.............................................:::......................................................................:) (:..............................:::.............................................:::......................................................................:) (:..............................:::.............................................:::......................................................................:) (:..............................:::.............................................:::......................................................................:) (:..............................:::.............................................:::......................................................................:) (:..............................:::.............................................:::......................................................................:) (:.............................:::::...........................................:::::.....................................................................:) (:..............................:::.............................................:::......................................................................:) (:...........................:...:...........:...............:...............:...:.......................................................................:) (:..................:::::::::::..............::..............::..............::..........................................................................:) (:..................::::::::::::....::::::::::::....::::::::::::....::::::::::::.........................................................................:) (:..................:::::::::::..............::..............::..............::..........................................................................:) (:...........................:...............:...............:...............:...........................................................................:) (:..............................................................................:::......................................................................:) (:..............................................................................:::......................................................................:) (:..............................................................................:::......................................................................:) (:..............................................................................:::......................................................................:) (:..............................................................................:::......................................................................:) (:..............................................................................:::......................................................................:) (:..............................................................................:::......................................................................:) (:..............................................................................:::......................................................................:) (:..............................................................................:::......................................................................:) (:.............................................................................:::::.....................................................................:) (:..............................................................................:::......................................................................:) (:...........................:...............:...............:...............:...:.......................................................................:) (:..................:::::::::::..............::..............::..............::..........................................................................:) (:..................::::::::::::....::::::::::::....::::::::::::....::::::::::::.........................................................................:) (:..................:::::::::::..............::..............::..............::..........................................................................:) (:...........................:...:...........:...............:...............:...........................................................................:) (:..............................:::.............................................:::......................................................................:) (:.............................:::::............................................:::......................................................................:) (:..............................:::.............................................:::......................................................................:) (:..............................:::.............................................:::......................................................................:) (:..............................:::.............................................:::......................................................................:) (:..............................:::.............................................:::......................................................................:) (:..............................:::.............................................:::......................................................................:) (:..............................:::.............................................:::......................................................................:) (:..............................:::.............................................:::......................................................................:) (:..............................:::............................................:::::.....................................................................:) (:..............................:::.............................................:::......................................................................:) (:...........:...............:...................................................:...........:...............:...............:...............:...........:) (:..:::::::::::.....:::::::::::.....................................................:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........:) (:..::::::::::::....::::::::::::....................................................::::::::::::....::::::::::::....::::::::::::....::::::::::::.........:) (:..:::::::::::.....:::::::::::.....................................................:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........:) (:...........:...............:...............................................................:...............:...............:...............:...........:) (:.......................................................................................................................................................:) (:.......................................................................................................................................................:) (:.......................................................................................................................................................:) (:.......................................................................................................................................................:) (:.......................................................................................................................................................:) (:.......................................................................................................................................................:) (:.......................................................................................................................................................:) (:.......................................................................................................................................................:) (:.......................................................................................................................................................:) (:.......................................................................................................................................................:) (:.......................................................................................................................................................:) (:.......................................................................................................................................................:) (:.......................................................................................................................................................:) (:.......................................................................................................................................................:) (:.......................................................................................................................................................:) (:.......................................................................................................................................................:) (:.......................................................................................................................................................:) (:.......................................................................................................................................................:) (:.......................................................................................................................................................:) (:.......................................................................................................................................................:) (:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::);
equal $cos_and_gate | distill-circuit $cos_and_image;
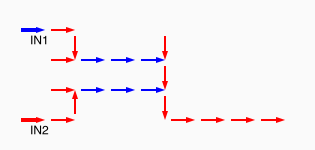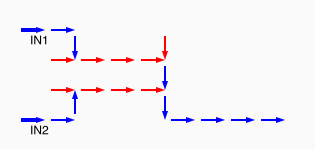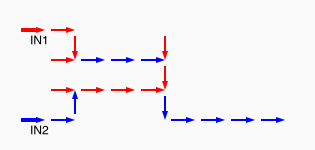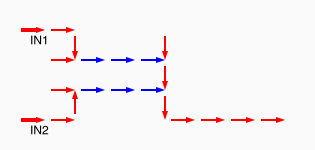
Run simulator
47. testing alternate primer based on gates: cos_or circuit
# This section contains one or more representations of a circuit # constructed using UNLESS gates.
define cos_or_gate | vector (vector 2 4 4 4 $true) (vector 2 6 4 6 $true) (vector 4 4 6 4 $true) (vector 4 6 6 6 $true) (vector 6 4 8 4 $true) (vector 6 6 8 6 $true) (vector 8 4 10 4 $true) (vector 8 6 10 6 $true) (vector 8 8 10 8 $true) (vector 10 2 10 4 $true) (vector 10 4 10 6 $false) (vector 10 6 10 8 $false) (vector 10 8 12 8 $true) (vector 12 8 14 8 $true) (vector 14 8 16 8 $true) (vector 16 8 18 8 $true);
define cos_or_image | make-image 93 169 | vector (:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:..............................................................................:::......................................................................................:) (:..............................................................................:::......................................................................................:) (:..............................................................................:::......................................................................................:) (:..............................................................................:::......................................................................................:) (:..............................................................................:::......................................................................................:) (:..............................................................................:::......................................................................................:) (:..............................................................................:::......................................................................................:) (:..............................................................................:::......................................................................................:) (:..............................................................................:::......................................................................................:) (:.............................................................................:::::.....................................................................................:) (:..............................................................................:::......................................................................................:) (:...........................:...............:...............:...............:...:.......................................................................................:) (:..................:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........................................................................................:) (:..................::::::::::::....::::::::::::....::::::::::::....::::::::::::.........................................................................................:) (:..................:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........................................................................................:) (:...........................:...............:...............:...............:...........................................................................................:) (:...............................................................................:.......................................................................................:) (:...............................................................................:.......................................................................................:) (:...............................................................................:.......................................................................................:) (:...............................................................................:.......................................................................................:) (:...............................................................................:.......................................................................................:) (:...............................................................................:.......................................................................................:) (:...............................................................................:.......................................................................................:) (:...............................................................................:.......................................................................................:) (:...............................................................................:.......................................................................................:) (:.............................................................................:::::.....................................................................................:) (:..............................................................................:::......................................................................................:) (:...........................:...............:...............:...............:...:.......................................................................................:) (:..................:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........................................................................................:) (:..................::::::::::::....::::::::::::....::::::::::::....::::::::::::.........................................................................................:) (:..................:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........................................................................................:) (:...........................:...............:...............:...............:...........................................................................................:) (:...............................................................................:.......................................................................................:) (:...............................................................................:.......................................................................................:) (:...............................................................................:.......................................................................................:) (:...............................................................................:.......................................................................................:) (:...............................................................................:.......................................................................................:) (:...............................................................................:.......................................................................................:) (:...............................................................................:.......................................................................................:) (:...............................................................................:.......................................................................................:) (:...............................................................................:.......................................................................................:) (:.............................................................................:::::.....................................................................................:) (:..............................................................................:::......................................................................................:) (:...........................................................................:...:...........:...............:...............:...............:...........................:) (:..................................................................:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........................:) (:..................................................................::::::::::::....::::::::::::....::::::::::::....::::::::::::....::::::::::::.........................:) (:..................................................................:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........................:) (:...........................................................................:...............:...............:...............:...............:...........................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::);
equal $cos_or_gate | distill-circuit $cos_or_image;
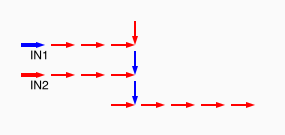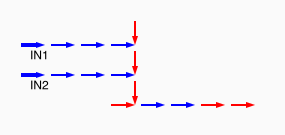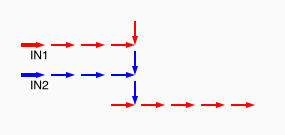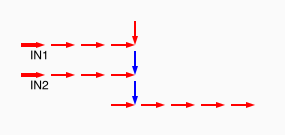
Run simulator
48. testing alternate primer based on gates: cos_nor circuit
# This section contains one or more representations of a circuit # constructed using UNLESS gates.
define cos_nor_gate | vector (vector 0 6 2 6 $true) (vector 0 8 2 8 $true) (vector 2 6 4 6 $true) (vector 2 8 4 8 $true) (vector 4 6 6 6 $true) (vector 4 8 6 8 $true) (vector 6 6 8 6 $true) (vector 6 8 8 8 $true) (vector 8 4 8 6 $true) (vector 8 6 8 8 $false) (vector 8 8 8 10 $false) (vector 8 10 10 10 $false) (vector 10 10 12 10 $false) (vector 12 10 14 10 $false) (vector 14 10 16 10 $false) (vector 16 10 18 10 $false) (vector 18 10 20 10 $false);
define cos_nor_image | make-image 125 169 | vector (:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:..............................................................:::......................................................................................................:) (:..............................................................:::......................................................................................................:) (:..............................................................:::......................................................................................................:) (:..............................................................:::......................................................................................................:) (:..............................................................:::......................................................................................................:) (:..............................................................:::......................................................................................................:) (:..............................................................:::......................................................................................................:) (:..............................................................:::......................................................................................................:) (:..............................................................:::......................................................................................................:) (:.............................................................:::::.....................................................................................................:) (:..............................................................:::......................................................................................................:) (:...........:...............:...............:...............:...:.......................................................................................................:) (:..:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........................................................................................................:) (:..::::::::::::....::::::::::::....::::::::::::....::::::::::::.........................................................................................................:) (:..:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........................................................................................................:) (:...........:...............:...............:...............:...........................................................................................................:) (:...............................................................:.......................................................................................................:) (:...............................................................:.......................................................................................................:) (:...............................................................:.......................................................................................................:) (:...............................................................:.......................................................................................................:) (:...............................................................:.......................................................................................................:) (:...............................................................:.......................................................................................................:) (:...............................................................:.......................................................................................................:) (:...............................................................:.......................................................................................................:) (:...............................................................:.......................................................................................................:) (:.............................................................:::::.....................................................................................................:) (:..............................................................:::......................................................................................................:) (:...........:...............:...............:...............:...:.......................................................................................................:) (:..:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........................................................................................................:) (:..::::::::::::....::::::::::::....::::::::::::....::::::::::::.........................................................................................................:) (:..:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........................................................................................................:) (:...........:...............:...............:...............:...........................................................................................................:) (:...............................................................:.......................................................................................................:) (:...............................................................:.......................................................................................................:) (:...............................................................:.......................................................................................................:) (:...............................................................:.......................................................................................................:) (:...............................................................:.......................................................................................................:) (:...............................................................:.......................................................................................................:) (:...............................................................:.......................................................................................................:) (:...............................................................:.......................................................................................................:) (:...............................................................:.......................................................................................................:) (:.............................................................:::::.....................................................................................................:) (:..............................................................:::......................................................................................................:) (:...............................................................:...........:...............:...............:...............:...............:...............:...........:) (:...........................................................................::..............::..............::..............::..............::..............::..........:) (:..................................................................::::::::::::....::::::::::::....::::::::::::....::::::::::::....::::::::::::....::::::::::::.........:) (:...........................................................................::..............::..............::..............::..............::..............::..........:) (:...........................................................................:...............:...............:...............:...............:...............:...........:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::);
equal $cos_nor_gate | distill-circuit $cos_nor_image;
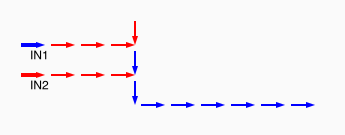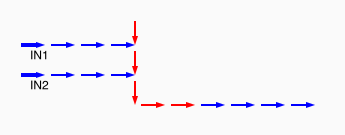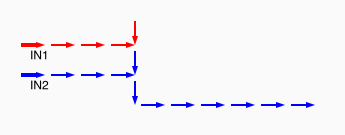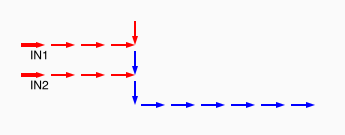
Run simulator
49. testing alternate primer based on gates: cos_osc circuit
# This section contains one or more representations of a circuit # constructed using UNLESS gates.
define cos_osc_gate | vector (vector 4 8 6 8 $true) (vector 6 8 8 8 $true) (vector 8 6 8 8 $true) (vector 10 6 8 6 $true) (vector 8 8 10 8 $false) (vector 12 6 10 6 $false) (vector 10 8 12 8 $false) (vector 12 8 12 6 $false) (vector 12 8 14 8 $false) (vector 14 8 16 8 $false);
define cos_osc_image | make-image 120 169 | vector (:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:...................................................................:...............:...................................................................................:) (:..................................................................:::::::::::.....::...................................................................................:) (:.................................................................::::::::::::....::::::::::::..........................................................................:) (:..................................................................:::::::::::.....::...................................................................................:) (:...................................................................:...............:...........:.......................................................................:) (:..............................................................:::.............................:::......................................................................:) (:..............................................................:::............................:::::.....................................................................:) (:..............................................................:::..............................:.......................................................................:) (:..............................................................:::..............................:.......................................................................:) (:..............................................................:::..............................:.......................................................................:) (:..............................................................:::..............................:.......................................................................:) (:..............................................................:::..............................:.......................................................................:) (:..............................................................:::..............................:.......................................................................:) (:..............................................................:::..............................:.......................................................................:) (:.............................................................:::::.............................:.......................................................................:) (:..............................................................:::..............................:.......................................................................:) (:...........................................:...............:...:...........:...............:...............:...............:...........................................:) (:..................................:::::::::::.....:::::::::::..............::..............::..............::..............::..........................................:) (:..................................::::::::::::....::::::::::::....::::::::::::....::::::::::::....::::::::::::....::::::::::::.........................................:) (:..................................:::::::::::.....:::::::::::..............::..............::..............::..............::..........................................:) (:...........................................:...............:...............:...............:...............:...............:...........................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::);
equal $cos_osc_gate | distill-circuit $cos_osc_image;
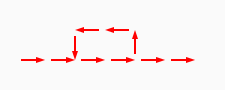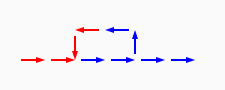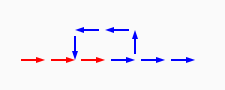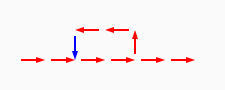
Run simulator
50. testing alternate primer based on gates: cos_sr circuit
# This section contains one or more representations of a circuit # constructed using UNLESS gates.
define cos_sr_gate | vector (vector 0 2 2 2 $true) (vector 0 8 2 8 $true) (vector 2 2 4 2 $true) (vector 2 8 4 8 $true) (vector 4 2 6 2 $true) (vector 4 6 6 6 $true) (vector 4 8 6 8 $true) (vector 6 8 6 6 $true) (vector 6 2 8 2 $true) (vector 6 6 8 6 $false) (vector 8 4 8 6 $false) (vector 8 2 10 2 $true) (vector 10 4 8 4 $false) (vector 8 6 10 6 $false) (vector 10 6 10 8 $false) (vector 10 2 12 2 $true) (vector 12 4 10 4 $false) (vector 10 6 12 6 $false) (vector 10 8 12 8 $false) (vector 12 6 12 4 $false) (vector 12 2 14 2 $true) (vector 14 4 12 4 $false) (vector 12 8 14 8 $false) (vector 14 2 14 4 $true) (vector 16 4 14 4 $true) (vector 14 8 16 8 $false) (vector 16 8 18 8 $false) (vector 18 8 20 8 $false);
define cos_sr_image | make-image 88 169 | vector (:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:...........:...............:...............:...............:...............:...............:...............:...........................................................:) (:..:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........................................................:) (:..::::::::::::....::::::::::::....::::::::::::....::::::::::::....::::::::::::....::::::::::::....::::::::::::.........................................................:) (:..:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........................................................:) (:...........:...............:...............:...............:...............:...............:...............:...........................................................:) (:..............................................................................................................:::......................................................:) (:..............................................................................................................:::......................................................:) (:..............................................................................................................:::......................................................:) (:..............................................................................................................:::......................................................:) (:..............................................................................................................:::......................................................:) (:..............................................................................................................:::......................................................:) (:..............................................................................................................:::......................................................:) (:..............................................................................................................:::......................................................:) (:..............................................................................................................:::......................................................:) (:.............................................................................................................:::::.....................................................:) (:..............................................................................................................:::......................................................:) (:...................................................................:...............:...............:...........:...:...................................................:) (:..................................................................::..............::..............::..............:::::::::::..........................................:) (:.................................................................::::::::::::....::::::::::::....::::::::::::....::::::::::::..........................................:) (:..................................................................::..............::..............::..............:::::::::::..........................................:) (:...................................................................:...............:...........:...:...............:...................................................:) (:...............................................................:..............................:::......................................................................:) (:...............................................................:.............................:::::.....................................................................:) (:...............................................................:...............................:.......................................................................:) (:...............................................................:...............................:.......................................................................:) (:...............................................................:...............................:.......................................................................:) (:...............................................................:...............................:.......................................................................:) (:...............................................................:...............................:.......................................................................:) (:...............................................................:...............................:.......................................................................:) (:...............................................................:...............................:.......................................................................:) (:.............................................................:::::.............................:.......................................................................:) (:..............................................................:::..............................:.......................................................................:) (:...........................................:...............:...:...........:...............:...........................................................................:) (:..................................:::::::::::..............::..............::..............::..........................................................................:) (:..................................::::::::::::....::::::::::::....::::::::::::....::::::::::::.........................................................................:) (:..................................:::::::::::..............::..............::..............::..........................................................................:) (:...........................................:...:...........:...............:...............:...........................................................................:) (:..............................................:::..............................:.......................................................................................:) (:.............................................:::::.............................:.......................................................................................:) (:..............................................:::..............................:.......................................................................................:) (:..............................................:::..............................:.......................................................................................:) (:..............................................:::..............................:.......................................................................................:) (:..............................................:::..............................:.......................................................................................:) (:..............................................:::..............................:.......................................................................................:) (:..............................................:::..............................:.......................................................................................:) (:..............................................:::..............................:.......................................................................................:) (:..............................................:::............................:::::.....................................................................................:) (:..............................................:::.............................:::......................................................................................:) (:...........:...............:...............:...................................:...........:...............:...............:...............:...............:...........:) (:..:::::::::::.....:::::::::::.....:::::::::::..............................................::..............::..............::..............::..............::..........:) (:..::::::::::::....::::::::::::....::::::::::::....................................::::::::::::....::::::::::::....::::::::::::....::::::::::::....::::::::::::.........:) (:..:::::::::::.....:::::::::::.....:::::::::::..............................................::..............::..............::..............::..............::..........:) (:...........:...............:...............:...............................................:...............:...............:...............:...............:...........:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::);
equal $cos_sr_gate | distill-circuit $cos_sr_image;
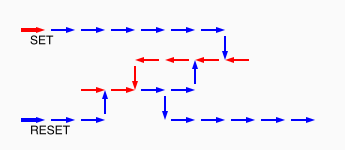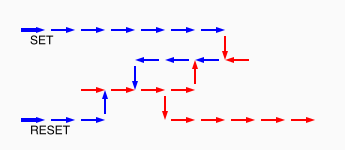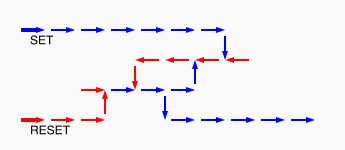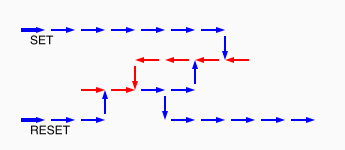
Run simulator
51. testing alternate primer based on gates: cos_d circuit
# This section contains one or more representations of a circuit # constructed using UNLESS gates.
define cos_d_gate | vector (vector 0 2 2 2 $true) (vector 0 6 2 6 $true) (vector 2 2 4 2 $true) (vector 2 6 4 6 $true) (vector 4 2 6 2 $true) (vector 4 6 6 6 $true) (vector 6 2 8 2 $true) (vector 6 6 8 6 $true) (vector 8 2 10 2 $true) (vector 8 6 10 6 $true) (vector 10 6 10 4 $true) (vector 10 10 10 8 $true) (vector 10 2 12 2 $true) (vector 10 4 12 4 $true) (vector 10 6 12 6 $true) (vector 10 8 12 8 $true) (vector 12 10 10 10 $true) (vector 12 0 12 2 $true) (vector 12 2 12 4 $false) (vector 12 6 12 8 $true) (vector 12 10 12 12 $true) (vector 12 4 14 4 $true) (vector 12 8 14 8 $false) (vector 14 10 12 10 $true) (vector 12 12 14 12 $true) (vector 14 0 14 2 $true) (vector 14 2 14 4 $true) (vector 14 4 14 6 $false) (vector 14 6 14 8 $false) (vector 14 8 14 10 $false) (vector 16 10 14 10 $true) (vector 14 12 16 12 $true) (vector 16 12 18 12 $true) (vector 18 12 20 12 $true);
define cos_d_image | make-image 109 169 | vector (:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:..............................................................................................:::.............:::......................................................:) (:..............................................................................................:::.............:::......................................................:) (:..............................................................................................:::.............:::......................................................:) (:..............................................................................................:::.............:::......................................................:) (:..............................................................................................:::.............:::......................................................:) (:..............................................................................................:::.............:::......................................................:) (:..............................................................................................:::.............:::......................................................:) (:..............................................................................................:::.............:::......................................................:) (:..............................................................................................:::.............:::......................................................:) (:.............................................................................................:::::...........:::::.....................................................:) (:..............................................................................................:::.............:::......................................................:) (:...........:...............:...............:...............:...............:...............:...:...............:.......................................................:) (:..:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........................................................................:) (:..::::::::::::....::::::::::::....::::::::::::....::::::::::::....::::::::::::....::::::::::::.........................................................................:) (:..:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........................................................................:) (:...........:...............:...............:...............:...............:...............:...........................................................................:) (:...............................................................................................:..............:::......................................................:) (:...............................................................................................:..............:::......................................................:) (:...............................................................................................:..............:::......................................................:) (:...............................................................................................:..............:::......................................................:) (:...............................................................................................:..............:::......................................................:) (:...............................................................................................:..............:::......................................................:) (:...............................................................................................:..............:::......................................................:) (:...............................................................................................:..............:::......................................................:) (:...............................................................................................:..............:::......................................................:) (:.............................................................................................:::::...........:::::.....................................................:) (:..............................................................................................:::.............:::......................................................:) (:...........................................................................................:...:...........:...:.......................................................:) (:..................................................................................:::::::::::.....:::::::::::..........................................................:) (:..................................................................................::::::::::::....::::::::::::.........................................................:) (:..................................................................................:::::::::::.....:::::::::::..........................................................:) (:...............................................................................:...........:...............:...........................................................:) (:..............................................................................:::..............................:.......................................................:) (:.............................................................................:::::.............................:.......................................................:) (:..............................................................................:::..............................:.......................................................:) (:..............................................................................:::..............................:.......................................................:) (:..............................................................................:::..............................:.......................................................:) (:..............................................................................:::..............................:.......................................................:) (:..............................................................................:::..............................:.......................................................:) (:..............................................................................:::..............................:.......................................................:) (:..............................................................................:::..............................:.......................................................:) (:..............................................................................:::............................:::::.....................................................:) (:..............................................................................:::.............................:::......................................................:) (:...........:...............:...............:...............:...............:...............:...................:.......................................................:) (:..:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........................................................................:) (:..::::::::::::....::::::::::::....::::::::::::....::::::::::::....::::::::::::....::::::::::::.........................................................................:) (:..:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........................................................................:) (:...........:...............:...............:...............:...............:...............:...........................................................................:) (:..............................................................................................:::..............:.......................................................:) (:..............................................................................................:::..............:.......................................................:) (:..............................................................................................:::..............:.......................................................:) (:..............................................................................................:::..............:.......................................................:) (:..............................................................................................:::..............:.......................................................:) (:..............................................................................................:::..............:.......................................................:) (:..............................................................................................:::..............:.......................................................:) (:..............................................................................................:::..............:.......................................................:) (:..............................................................................................:::..............:.......................................................:) (:.............................................................................................:::::...........:::::.....................................................:) (:..............................................................................................:::.............:::......................................................:) (:...........................................................................................:...:...........:...:.......................................................:) (:..................................................................................:::::::::::..............::..........................................................:) (:..................................................................................::::::::::::....::::::::::::.........................................................:) (:..................................................................................:::::::::::..............::..........................................................:) (:...............................................................................:...........:...............:...........................................................:) (:..............................................................................:::..............................:.......................................................:) (:.............................................................................:::::.............................:.......................................................:) (:..............................................................................:::..............................:.......................................................:) (:..............................................................................:::..............................:.......................................................:) (:..............................................................................:::..............................:.......................................................:) (:..............................................................................:::..............................:.......................................................:) (:..............................................................................:::..............................:.......................................................:) (:..............................................................................:::..............................:.......................................................:) (:..............................................................................:::..............................:.......................................................:) (:..............................................................................:::............................:::::.....................................................:) (:..............................................................................:::.............................:::......................................................:) (:...................................................................................:...............:...........:...:...................................................:) (:..................................................................................:::::::::::.....:::::::::::.....:::::::::::..........................................:) (:.................................................................................::::::::::::....::::::::::::....::::::::::::..........................................:) (:..................................................................................:::::::::::.....:::::::::::.....:::::::::::..........................................:) (:...................................................................................:...............:...............:...................................................:) (:..............................................................................................:::......................................................................:) (:..............................................................................................:::......................................................................:) (:..............................................................................................:::......................................................................:) (:..............................................................................................:::......................................................................:) (:..............................................................................................:::......................................................................:) (:..............................................................................................:::......................................................................:) (:..............................................................................................:::......................................................................:) (:..............................................................................................:::......................................................................:) (:..............................................................................................:::......................................................................:) (:.............................................................................................:::::.....................................................................:) (:..............................................................................................:::......................................................................:) (:...............................................................................................:...........:...............:...............:...............:...........:) (:..................................................................................................:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........:) (:..................................................................................................::::::::::::....::::::::::::....::::::::::::....::::::::::::.........:) (:..................................................................................................:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........:) (:...........................................................................................................:...............:...............:...............:...........:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:.......................................................................................................................................................................:) (:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::);
equal $cos_d_gate | distill-circuit $cos_d_image;
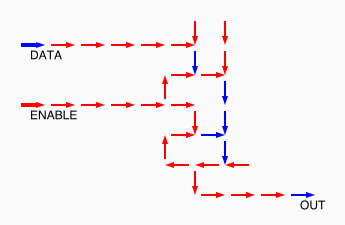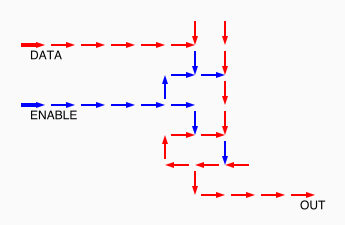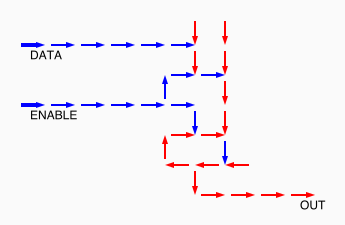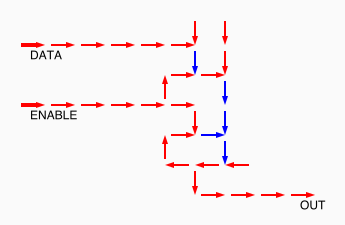
Run simulator
52. probing networks of unless gates
define set-input | ? circuit | ? index | ? value | assign wire (list-ref $circuit $index) | map (? w | if (not | equal $w $wire) $w | vector (list-ref $w 0) (list-ref $w 1) (list-ref $w 2) (list-ref $w 3) $value) $circuit;
define read-output | ? circuit | ? index | assign len (list-length $circuit) | assign wire (list-ref $circuit | - (- $len 1) $index) | list-ref $wire 4;
define sim | ? circuit | ? steps | ? setter | if (= $steps 0) $circuit | sim (simulate-unless | setter $circuit) (- $steps 1) $setter;
define smart-sim | ? circuit | ? setter | sim $circuit (list-length $circuit) $setter;
# test cos_not gate
define cos_not_harness | ? x | assign c $cos_not_gate | assign c (smart-sim $c | ? c | set-input $c 0 $x) | read-output $c 0;
# test cos_and gate
define cos_and_harness | ? x | ? y | assign c $cos_and_gate | assign c (smart-sim $c | ? c | set-input (set-input $c 0 $x) 1 $y) | read-output $c 0;
= $false | cos_and_harness $false $false;
# this code is more awkward than it needs to be - # should make circuits mutable
53. end of part 3, start of part 4
# The following parts of the message start # to introduce some self-reference into the message
54. a mechanism for referring to parts of the message
# Many choices for how to do this. # Could do it without special machinery by using the # standard A-B trick for giving e.g. a Turing machine # access to its own description. # Instead, will simply introduce a "primer" function # that gives access to every statement made so far # (question: should future statements be included? # tentatively assume YES: will simplify # discussion of creating modified copies of the # complete message).
# For now, assume primer is a list of statements, # with each statement being a list in the same # form as "translate" functions expect. # This means that there is, for now, no # distinction between unary or binary, # and the "|" structure is expanded.
# this line is referred to later - change/move carefully
equal (list-ref $primer 0) | vector intro unary;
equal (list-ref $primer 1) | vector intro is;
equal (list-ref $primer 2) | vector intro int;
equal (list-ref $primer 3) | vector is int | vector unary 0;
equal (list-ref $primer 4) | vector is int | vector unary 1 0;
assign idx (list:find $primer | vector intro primer) | equal (list-ref $primer | + $idx 1) | quote @@ | equal (list-ref $primer 0) | vector intro unary;
# Now, we could return to the MUD, simulate an agent A # transferring a copy of the primer to another agent B, # and then show B making a modified copy of that primer # and passing it back to A.
# We could also show agents experimenting with the # primer in various ways.
# Message is pretty solid up to this point. # For testing purposes, useful to save state here to disk, # command: DISK-SAVE base
55. some preparatory work for integrating with Java code
class Object () (method add-one | ? x | + $x 1) (method unknown | ? x $x) (method <init>-V $self) (method <init> $self) (method classname Object) (method equals-Object-Z | this ==) (method equals | self equals-Object-Z) (method act $true) (method isobj $true);
# inconsistency of various kinds of equality throughout message # needs to be cleaned up
class Integer () (field super | java-object new) (field value | cell new 0) (method <init> $self) (method <init>-V $self) (method <init>-I-V | ? v | begin (value set $v) $self) (method intValue-V | value get) (method intValue | self intValue-V) (method equals-Object-Z | ? o | if (not | = Integer | o classname) $false | = (value get) (o value get)) (method equals | self equals-Object-Z) (method get | value get) (method set | ? x | value set | if (not | function? $x) $x | x intValue) (method classname Integer) (method unknown | ? x | super $x);
# string is basically the same as an integer
class String () (field super | java-object new) (field value | cell new 0) (method <init> $self) (method <init>-V $self) (method <init>-String-V | ? v | begin (value set | v value get) $self) (method int-init | ? x | begin (value set $x) $self) (method intValue-V | value get) (method intValue | self intValue-V) (method equals-Object-Z | ? o | if (not | = String | o classname) $false | = (value get) (o value get)) (method equals | self equals-Object-Z) (method get | value get) (method set | ? x | value set | if (not | function? $x) $x | x intValue) (method classname String) (method unknown | ? x | super $x);
# will need to install class hierarchy, just hardcode a few things for now
define java | ? x | ? y | cond ((= $y String) $String) ((= $y Object) $java-object) ((= $y Integer) $Integer) $java-object;
= ((java util String) new add-one 15) 16;
class java-numeric () (field super (java-object new)) (method unknown | ? x | super $x) (field java-content | cell new 0) (method get | java-content get) (method init | ? v | begin (self set $v) $self) (method set | ? v | java-content set $v);
define state-machine-test1 | ? x | cond ((= $x 1) 20) ((= $x 2) 40) ((= $x 3) 60) 0;
define state-machine-test2 | ? x | cond ((= $x 1) | java-test1 set 20) ((= $x 2) | java-test1 set 40) ((= $x 3) | java-test1 set 60) 0;
define compare-object-reference | ? o1 | ? o2 | if (not | function? $o1) (not | function? $o2) | = (o1 unique-id) (o2 unique-id);
define jvm-maker | lambda (vars stack pc ret) | ? op | begin (pc set | + (pc get) 1) | cond ((= $op new) | ? type | stack-push $stack | $type new) ((= $op dup) | stack-push $stack | stack-peek $stack) ((= $op checkcast) | ? t 1) ((or (= $op astore) (= $op istore)) | ? index | vars set | hash-add (vars get) $index | stack-pop $stack) ((or (= $op aload) (= $op iload)) | ? index | stack-push $stack | hash-ref (vars get) $index) ((or (= $op iconst) (= $op ldc)) | ? val | stack-push $stack $val) ((= $op aconst_null) | stack-push $stack 0) ((= $op instanceof) | ? t | stack-push $stack | function? | (stack-pop $stack) (t new classname)) ((= $op getfield) | ? key | ? ignore | stack-push $stack | (stack-pop $stack) $key get) ((= $op putfield) | ? key | ? ignore | assign val (stack-pop $stack) | (stack-pop $stack) $key set $val) ((= $op imul) | assign v2 (stack-pop $stack) | assign v1 (stack-pop $stack) | stack-push $stack | * $v1 $v2) ((= $op iadd) | assign v2 (stack-pop $stack) | assign v1 (stack-pop $stack) | stack-push $stack | + $v1 $v2) ((= $op isub) | assign v2 (stack-pop $stack) | assign v1 (stack-pop $stack) | stack-push $stack | - $v1 $v2) ((= $op goto) | ? x | pc set $x) ((= $op iflt) | ? x | if (< (stack-pop $stack) 0) (pc set $x) 0) ((= $op ifle) | ? x | if (<= (stack-pop $stack) 0) (pc set $x) 0) ((= $op ifgt) | ? x | if (> (stack-pop $stack) 0) (pc set $x) 0) ((= $op ifge) | ? x | if (>= (stack-pop $stack) 0) (pc set $x) 0) ((= $op ifne) | ? x | if (not | = (stack-pop $stack) 0) (pc set $x) 0) ((= $op ifeq) | ? x | if (= (stack-pop $stack) 0) (pc set $x) 0) ((= $op if_icmpne) | ? x | assign v2 (stack-pop $stack) | assign v1 (stack-pop $stack) | if (not | = $v1 $v2) (pc set $x) 0) ((= $op if_icmpeq) | ? x | assign v2 (stack-pop $stack) | assign v1 (stack-pop $stack) | if (= $v1 $v2) (pc set $x) 0) ((= $op if_acmpne) | ? x | assign v2 (stack-pop $stack) | assign v1 (stack-pop $stack) | if (not | compare-object-reference $v1 $v2) (pc set $x) 0) ((= $op if_acmpeq) | ? x | assign v2 (stack-pop $stack) | assign v1 (stack-pop $stack) | if (compare-object-reference $v1 $v2) (pc set $x) 0) ((= $op if_icmpge) | ? x | assign v2 (stack-pop $stack) | assign v1 (stack-pop $stack) | if (>= $v1 $v2) (pc set $x) 0) ((= $op if_icmpgt) | ? x | assign v2 (stack-pop $stack) | assign v1 (stack-pop $stack) | if (> $v1 $v2) (pc set $x) 0) ((= $op if_icmple) | ? x | assign v2 (stack-pop $stack) | assign v1 (stack-pop $stack) | if (<= $v1 $v2) (pc set $x) 0) ((= $op if_icmplt) | ? x | assign v2 (stack-pop $stack) | assign v1 (stack-pop $stack) | if (< $v1 $v2) (pc set $x) 0) ((= $op ifnull) | ? x | if (not | function? | stack-pop $stack) (pc set $x) 0) ((= $op ifnonnull) | ? x | if (function? | stack-pop $stack) (pc set $x) 0) ((= $op return) | begin (ret set | hash-ref (vars get) 0) (pc set $minus-one)) ((= $op ireturn) | begin (ret set | stack-pop $stack) (pc set $minus-one)) ((= $op areturn) | begin (ret set | stack-pop $stack) (pc set $minus-one)) ((= $op invokevirtual) | lambda (target m n) | assign result (stack-call $stack $target $m) | if (not | = $n 1) 0 | stack-push $stack $result) ((= $op invokeinterface) | lambda (target m n ignore) | assign result (stack-call $stack $target $m) | if (not | = $n 1) 0 | stack-push $stack $result) ((= $op invokespecial) | lambda (target m n) | assign result (stack-call-special $stack (hash-ref (vars get) 0) $target $m) | if (not | = $n 1) 0 | stack-push $stack $result) 0;
define stack-call | lambda (stack target ct) | if (= $ct 0) ((stack-pop $stack) $target) (assign arg (stack-pop $stack) | (stack-call $stack $target (- $ct 1)) $arg);
define stack-call-special | lambda (stack self target ct) | if (= (ct) 0) (let ((act | stack-pop $stack)) | if (act == $self) (act super $target) (act $target)) (let ((arg | stack-pop $stack)) | (stack-call-special $stack $self $target (- $ct 1)) $arg);
define stack-push | lambda (stack x) | stack set | prepend $x | stack get;
define stack-pop | lambda (stack) | let ((v | head | stack get)) | begin (stack set | tail | stack get) $v;
define stack-peek | lambda (stack) | head | stack get;
define stack-test1 | cell new | vector 5 3 1;
define test-jvm | jvm-maker $vars-test1 $stack-test1 $pc-test1 $ret-test1;
class test-class () (field x | int new) (field y | int new);
define state-machine-helper | ? at | lambda (vars stack machine) | let ((pc | cell new $at) (ret | cell new $true)) | let ((jvm | jvm-maker $vars $stack $pc $ret)) | begin (machine $jvm | pc get) (if (= (pc get) $minus-one) (ret get) | state-machine-helper (pc get) $vars $stack $machine);
define state-machine | state-machine-helper 0;
= 33 | state-machine $vars-test1 $stack-test1 | ? jvm | ? x | cond ((= $x 0) | jvm istore 4) ((= $x 1) | jvm iload 4) (jvm ireturn);
define bytecode-test-mul | lambda (arg0 arg1) | let ((vars | cell new | make-hash | vector (pair 0 0) (pair 1 $arg0) (pair 2 $arg1)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= (x) 0) | jvm iload 1) ((= (x) 1) | jvm iload 2) ((= (x) 2) | jvm imul) ((= (x) 3) | jvm ireturn) (jvm return);
56. class translation 'COS_JavaTest'
# Produced by Fritzifier, based on JasminVisitor
# Using BCEL library to read Java bytecode
# Here is the original code:
# public class COS_JavaTest {
# private int q = 0;
# public int add(int x, int y) {
# return x + y;
# }
# public int sub(int x, int y) {
# return x - y;
# }
# public int mult(int x, int y) {
# return x * y;
# }
# public int addmult(int x, int y, int z) {
# return add(x, mult(y, z));
# }
# public void set(int x) {
# q = x;
# }
# public int get() {
# return q;
# }
# public int fact(int x) {
# return ( x> 0) ? (x * fact(sub(x, 1))) : 1;
# }
# }
class COS_JavaTest () (field super-ref | make-cell 0) (method new | set! $super-ref | (java lang Object) $this) (method super | ? x | (get! $super-ref) $x) (method unknown | ? x | self super $x) (field q | (int) new) (method <init>-V (lambda () | let ((vars | cell new | make-hash | vector (pair 0 $self)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm aload 0) ((= $x 1) | jvm invokespecial <init>-V 0 0) ((= $x 2) | jvm aload 0) ((= $x 3) | jvm iconst 0) ((= $x 4) | jvm putfield q $int) ((= $x 5) | jvm return) (jvm return)) ) (method <init> | self <init>-V) (method add-I-I-I (lambda (arg0 arg1) | let ((vars | cell new | make-hash | vector (pair 0 $self) (pair 1 $arg0) (pair 2 $arg1)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm iload 1) ((= $x 1) | jvm iload 2) ((= $x 2) | jvm iadd) ((= $x 3) | jvm ireturn) (jvm return)) ) (method add | self add-I-I-I) (method sub-I-I-I (lambda (arg0 arg1) | let ((vars | cell new | make-hash | vector (pair 0 $self) (pair 1 $arg0) (pair 2 $arg1)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm iload 1) ((= $x 1) | jvm iload 2) ((= $x 2) | jvm isub) ((= $x 3) | jvm ireturn) (jvm return)) ) (method sub | self sub-I-I-I) (method mult-I-I-I (lambda (arg0 arg1) | let ((vars | cell new | make-hash | vector (pair 0 $self) (pair 1 $arg0) (pair 2 $arg1)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm iload 1) ((= $x 1) | jvm iload 2) ((= $x 2) | jvm imul) ((= $x 3) | jvm ireturn) (jvm return)) ) (method mult | self mult-I-I-I) (method addmult-I-I-I-I (lambda (arg0 arg1 arg2) | let ((vars | cell new | make-hash | vector (pair 0 $self) (pair 1 $arg0) (pair 2 $arg1) (pair 3 $arg2)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm aload 0) ((= $x 1) | jvm iload 1) ((= $x 2) | jvm aload 0) ((= $x 3) | jvm iload 2) ((= $x 4) | jvm iload 3) ((= $x 5) | jvm invokevirtual mult-I-I-I 2 1) ((= $x 6) | jvm invokevirtual add-I-I-I 2 1) ((= $x 7) | jvm ireturn) (jvm return)) ) (method addmult | self addmult-I-I-I-I) (method set-I-V (lambda (arg0) | let ((vars | cell new | make-hash | vector (pair 0 $self) (pair 1 $arg0)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm aload 0) ((= $x 1) | jvm iload 1) ((= $x 2) | jvm putfield q $int) ((= $x 3) | jvm return) (jvm return)) ) (method set | self set-I-V) (method get-I (lambda () | let ((vars | cell new | make-hash | vector (pair 0 $self)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm aload 0) ((= $x 1) | jvm getfield q $int) ((= $x 2) | jvm ireturn) (jvm return)) ) (method get | self get-I) (method fact-I-I (lambda (arg0) | let ((vars | cell new | make-hash | vector (pair 0 $self) (pair 1 $arg0)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm iload 1) ((= $x 1) | jvm ifle 11) ((= $x 2) | jvm iload 1) ((= $x 3) | jvm aload 0) ((= $x 4) | jvm aload 0) ((= $x 5) | jvm iload 1) ((= $x 6) | jvm iconst 1) ((= $x 7) | jvm invokevirtual sub-I-I-I 2 1) ((= $x 8) | jvm invokevirtual fact-I-I 1 1) ((= $x 9) | jvm imul) ((= $x 10) | jvm goto 12) ((= $x 11) | jvm iconst 1) ((= $x 12) | jvm ireturn) (jvm return)) ) (method fact | self fact-I-I) ;
57. check that automatic conversion is workable
# Note that the names of methods include type information. # This could easily be removed, but is retained so that overloading # is possible in the Java code. # I is integer, V is void. The last type in the name is the return type.
# The type information can be safely omitted if there is no ambiguity
= (test1 addmult-I-I-I-I 4 15 10) 154;
begin (test1 set-I-V 87) (= (test1 get-I) 87);
# Yay! testing says this works. # So structure for bytecode interpretation is in place. # Very few opcodes actually implemented yet though.
58. another simple little text-adventure space
# let us try to make a slightly more interesting world
define make-table | ? lst | reduce (? x | ? h | assign name (car $x) | assign obj (cdr $x) | hash-add $h $name $obj) (append $hash-null $lst);
# note, the quoted strings below are just represented as a big number, # nothing special
define geo-map | make-table | map (? name | cons $name | room new $name) (vector "boston" "dublin" "paris" "genoa");
define my-links | map (? entry | assign src (car $entry) | assign dest (cdr $entry) | door new (geo-map $src) (geo-map $dest)) (vector (cons "boston" "dublin") (cons "dublin" "paris") (cons "boston" "paris") (cons "paris" "genoa"));
myrobo set-room | geo-map "dublin";
equal "dublin" | myrobo get-room name;
equal "paris" | myrobo get-room name;
equal "genoa" | myrobo get-room name;
equal "paris" | myrobo get-room name;
equal "boston" | myrobo get-room name;
equal "dublin" | myrobo get-room name;
equal "paris" | myrobo get-room name;
# all characters should update together
class world (the-places the-links) (field things | container new) (field names | cell new $hash-null) (field places | cell new 0) (field links | cell new 0) (method new | begin (places set | make-table | map (? name | cons $name | room new $name) $the-places) (links set | map (? entry | assign src (car $entry) | assign dest (cdr $entry) | door new (places get $src) (places get $dest)) $the-links)) (method add | lambda (place name val) | begin (val set-room | places get $place) (val set-name $name) (names set | hash-add (names get) $name $val) (things add $val)) (method find | ? n | names get $n get-room name) (method reachable | ? place | assign exits (select-match (instanceof door) | places get $place inventory) | map (? door | door access-from (places get $place) name) $exits) (method update | begin (map (? x | x update) | things inventory) $true);
define geo-world | world new (vector "boston" "dublin" "paris" "genoa") (vector (cons "boston" "dublin") (cons "dublin" "paris") (cons "boston" "paris") (cons "paris" "genoa"));
geo-world add "dublin" "robo1" | robo new;
geo-world add "genoa" "robo2" | robo new;
equal "dublin" | geo-world find "robo1";
equal "genoa" | geo-world find "robo2";
equal "paris" | geo-world find "robo1";
equal "paris" | geo-world find "robo2";
equal (vector "paris" "dublin") | geo-world reachable "boston";
equal (vector "paris") | geo-world reachable "genoa";
59. native implementation of a Java list, hash classes
define flex-equals (lambda (x y) (if (not | function? | x) (if (not | function? | y) (= (x) (y)) (false)) (if (not | function? | y) (false) (x equals (y)))));
define remove-object (lambda (x) (remove-match (lambda (y) (flex-equals (x) (y)))));
define contains-object (lambda (x lst) (if (> (list-length | lst) 0) (if (flex-equals (head | lst) (x)) (true) (contains-object (x) (tail | lst))) (false)));
class COS_JList () (field super ((java lang Object) new)) (method unknown (lambda (x) (super (x)))) (field contents (cell new (vector))) (method <init>-V (self)) (method <init> (self <init>-V)) (method add-Object-V (lambda (x) (contents set (prepend (x) (contents get))))) (method add (self add-Object-V)) (method remove-Object-Z (lambda (x) (contents set (remove-object (x) (contents get))))) (method remove (self remove-Object-Z)) (method contains-Object-Z (lambda (x) (contains-object (x) (contents get)))) (method contains (self contains-Object-Z)) (method get-I-Object (lambda (x) (list-ref (contents get) (x)))) (method get (self get-I-Object)) (method iterator-Iterator (COS_JListIterator new (self))) (method iterator (self iterator-Iterator)) (method size-V-I (list-length (contents get))) (method size (self size-V-I));
begin (test1 add-Object-V (test1)) (= 1 | test1 size-V-I);
class COS_JHashMap () (field super ((java lang Object) new)) (method unknown (lambda (x) (super (x)))) (field contents (cell new (? x 0))) (method <init>-V (self)) (method <init> (self <init>-V)) (method put-Object-Object-V (lambda (x y) (let ((prev | contents get)) (contents set (? z (if (flex-equals (z) (x)) (y) (prev (z)))))))) (method put (self put-Object-Object-V)) (method get-Object-Object (lambda (x) (contents get (x)))) (method get (self get-Object-Object));
begin (test2 put-Object-Object-V 5 10) (= 10 | test2 get 5);
# There is Java code for COS_JList available
# There is Java code for COS_JHashMap available
60. testing the JList class
begin (test1 add-Object-V (test1)) (= 1 (test1 size-V-I));
61. basic iterator implementation
class COS_JListIterator (ref) (field pipe (cell new (ref contents get))) (method <init>-V (self)) (method <init> (self <init>-V)) (method hasNext-Z (> (list-length | pipe get) 0)) (method hasNext (self hasNext-Z)) (method next (self next-Object)) (method next-Object (let ((result (head | pipe get))) (begin (pipe set | tail | pipe get) (result))));
begin (test1 add 15) (test1 add 72) (test1 add 99) (true);
# There is Java code for COS_JListIterator available
62. class translation 'COS_JDoor'
# Produced by Fritzifier, based on JasminVisitor
# Using BCEL library to read Java bytecode
# Here is the original code:
#
# public class COS_JDoor {
# private COS_JRoom src, dest;
# private String src_cmd, dest_cmd;
#
# public COS_JDoor(COS_JRoom src, String src_cmd,
# COS_JRoom dest, String dest_cmd) {
# this.src = src;
# this.dest = dest;
# this.src_cmd = src_cmd;
# this.dest_cmd = dest_cmd;
# src.addDoor(this);
# dest.addDoor(this);
# }
#
# public COS_JRoom apply(COS_JRoom src, String cmd) {
# if (src == this.src) {
# if (src_cmd.equals(cmd)) {
# return this.dest;
# }
# }
# if (src == this.dest) {
# if (dest_cmd.equals(cmd)) {
# return this.src;
# }
# }
# return null;
# }
#
# public COS_JRoom apply(COS_JRoom src) {
# if (src==this.src) {
# return this.dest;
# }
# if (src==this.dest) {
# return this.src;
# }
# return null;
# }
# }
class COS_JDoor () (field super-ref | make-cell 0) (method new | set! $super-ref | (java lang Object) $this) (method super | ? x | (get! $super-ref) $x) (method unknown | ? x | self super $x) (field src | cell new 0) (field dest | cell new 0) (field src_cmd | cell new 0) (field dest_cmd | cell new 0) (method <init>-COS_JRoom-String-COS_JRoom-String-V (lambda (arg0 arg1 arg2 arg3) | let ((vars | cell new | make-hash | vector (pair 0 $self) (pair 1 $arg0) (pair 2 $arg1) (pair 3 $arg2) (pair 4 $arg3)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm aload 0) ((= $x 1) | jvm invokespecial <init>-V 0 0) ((= $x 2) | jvm aload 0) ((= $x 3) | jvm aload 1) ((= $x 4) | jvm putfield src $COS_JRoom) ((= $x 5) | jvm aload 0) ((= $x 6) | jvm aload 3) ((= $x 7) | jvm putfield dest $COS_JRoom) ((= $x 8) | jvm aload 0) ((= $x 9) | jvm aload 2) ((= $x 10) | jvm putfield src_cmd (java lang String)) ((= $x 11) | jvm aload 0) ((= $x 12) | jvm aload 4) ((= $x 13) | jvm putfield dest_cmd (java lang String)) ((= $x 14) | jvm aload 1) ((= $x 15) | jvm aload 0) ((= $x 16) | jvm invokevirtual addDoor-COS_JDoor-V 1 0) ((= $x 17) | jvm aload 3) ((= $x 18) | jvm aload 0) ((= $x 19) | jvm invokevirtual addDoor-COS_JDoor-V 1 0) ((= $x 20) | jvm return) (jvm return)) ) (method <init> | self <init>-COS_JRoom-String-COS_JRoom-String-V) (method apply-COS_JRoom-String-COS_JRoom (lambda (arg0 arg1) | let ((vars | cell new | make-hash | vector (pair 0 $self) (pair 1 $arg0) (pair 2 $arg1)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm aload 1) ((= $x 1) | jvm aload 0) ((= $x 2) | jvm getfield src $COS_JRoom) ((= $x 3) | jvm if_acmpne 12) ((= $x 4) | jvm aload 0) ((= $x 5) | jvm getfield src_cmd (java lang String)) ((= $x 6) | jvm aload 2) ((= $x 7) | jvm invokevirtual equals-Object-Z 1 1) ((= $x 8) | jvm ifeq 12) ((= $x 9) | jvm aload 0) ((= $x 10) | jvm getfield dest $COS_JRoom) ((= $x 11) | jvm areturn) ((= $x 12) | jvm aload 1) ((= $x 13) | jvm aload 0) ((= $x 14) | jvm getfield dest $COS_JRoom) ((= $x 15) | jvm if_acmpne 24) ((= $x 16) | jvm aload 0) ((= $x 17) | jvm getfield dest_cmd (java lang String)) ((= $x 18) | jvm aload 2) ((= $x 19) | jvm invokevirtual equals-Object-Z 1 1) ((= $x 20) | jvm ifeq 24) ((= $x 21) | jvm aload 0) ((= $x 22) | jvm getfield src $COS_JRoom) ((= $x 23) | jvm areturn) ((= $x 24) | jvm aconst_null) ((= $x 25) | jvm areturn) (jvm return)) ) (method apply | self apply-COS_JRoom-String-COS_JRoom) (method apply-COS_JRoom-COS_JRoom (lambda (arg0) | let ((vars | cell new | make-hash | vector (pair 0 $self) (pair 1 $arg0)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm aload 1) ((= $x 1) | jvm aload 0) ((= $x 2) | jvm getfield src $COS_JRoom) ((= $x 3) | jvm if_acmpne 7) ((= $x 4) | jvm aload 0) ((= $x 5) | jvm getfield dest $COS_JRoom) ((= $x 6) | jvm areturn) ((= $x 7) | jvm aload 1) ((= $x 8) | jvm aload 0) ((= $x 9) | jvm getfield dest $COS_JRoom) ((= $x 10) | jvm if_acmpne 14) ((= $x 11) | jvm aload 0) ((= $x 12) | jvm getfield src $COS_JRoom) ((= $x 13) | jvm areturn) ((= $x 14) | jvm aconst_null) ((= $x 15) | jvm areturn) (jvm return)) ) ;
63. class translation 'COS_JThing'
# Produced by Fritzifier, based on JasminVisitor
# Using BCEL library to read Java bytecode
# Here is the original code:
#
# public class COS_JThing extends COS_JNamed {
# private COS_JRoom location;
# private COS_JRoom nextLocation;
#
# public void setRoom(COS_JRoom location) {
# if (this.location!=null) {
# this.location.removeThing(this);
# }
# this.location = location;
# location.addThing(this);
# this.nextLocation = location;
# }
#
# public COS_JRoom getRoom() {
# return location;
# }
#
# public void setNextRoom(COS_JRoom location) {
# nextLocation = location;
# }
#
# public void postUpdate() {
# if (nextLocation!=location) {
# setRoom(nextLocation);
# }
# }
# }
#
class COS_JThing () (field super-ref | make-cell 0) (method new | set! $super-ref | (COS_JNamed) $this) (method super | ? x | (get! $super-ref) $x) (method unknown | ? x | self super $x) (field location | cell new 0) (field nextLocation | cell new 0) (method <init>-V (lambda () | let ((vars | cell new | make-hash | vector (pair 0 $self)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm aload 0) ((= $x 1) | jvm invokespecial <init>-V 0 0) ((= $x 2) | jvm return) (jvm return)) ) (method <init> | self <init>-V) (method setRoom-COS_JRoom-V (lambda (arg0) | let ((vars | cell new | make-hash | vector (pair 0 $self) (pair 1 $arg0)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm aload 0) ((= $x 1) | jvm getfield location $COS_JRoom) ((= $x 2) | jvm ifnull 7) ((= $x 3) | jvm aload 0) ((= $x 4) | jvm getfield location $COS_JRoom) ((= $x 5) | jvm aload 0) ((= $x 6) | jvm invokevirtual removeThing-COS_JThing-V 1 0) ((= $x 7) | jvm aload 0) ((= $x 8) | jvm aload 1) ((= $x 9) | jvm putfield location $COS_JRoom) ((= $x 10) | jvm aload 1) ((= $x 11) | jvm aload 0) ((= $x 12) | jvm invokevirtual addThing-COS_JThing-V 1 0) ((= $x 13) | jvm aload 0) ((= $x 14) | jvm aload 1) ((= $x 15) | jvm putfield nextLocation $COS_JRoom) ((= $x 16) | jvm return) (jvm return)) ) (method setRoom | self setRoom-COS_JRoom-V) (method getRoom-COS_JRoom (lambda () | let ((vars | cell new | make-hash | vector (pair 0 $self)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm aload 0) ((= $x 1) | jvm getfield location $COS_JRoom) ((= $x 2) | jvm areturn) (jvm return)) ) (method getRoom | self getRoom-COS_JRoom) (method setNextRoom-COS_JRoom-V (lambda (arg0) | let ((vars | cell new | make-hash | vector (pair 0 $self) (pair 1 $arg0)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm aload 0) ((= $x 1) | jvm aload 1) ((= $x 2) | jvm putfield nextLocation $COS_JRoom) ((= $x 3) | jvm return) (jvm return)) ) (method setNextRoom | self setNextRoom-COS_JRoom-V) (method postUpdate-V (lambda () | let ((vars | cell new | make-hash | vector (pair 0 $self)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm aload 0) ((= $x 1) | jvm getfield nextLocation $COS_JRoom) ((= $x 2) | jvm aload 0) ((= $x 3) | jvm getfield location $COS_JRoom) ((= $x 4) | jvm if_acmpeq 9) ((= $x 5) | jvm aload 0) ((= $x 6) | jvm aload 0) ((= $x 7) | jvm getfield nextLocation $COS_JRoom) ((= $x 8) | jvm invokevirtual setRoom-COS_JRoom-V 1 0) ((= $x 9) | jvm return) (jvm return)) ) (method postUpdate | self postUpdate-V) ;
64. class translation 'COS_JRoom'
# Produced by Fritzifier, based on JasminVisitor
# Using BCEL library to read Java bytecode
# Here is the original code:
#
# import java.util.Iterator;
#
# public class COS_JRoom extends COS_JNamed {
# //private COS_JList content = new COS_JList();
# //private COS_JList doors = new COS_JList();
#
# private COS_JList content;
# private COS_JList doors;
#
# public COS_JRoom() {
# content = new COS_JList();
# doors = new COS_JList();
# }
#
# public COS_JList get() {
# return content;
# }
#
# public Iterator getDoors() {
# return doors.iterator();
# }
#
# public void addDoor(COS_JDoor door) {
# //System.out.println("add door -> " + getName());
# doors.add(door);
# }
#
# public void addThing(COS_JThing thing) {
# content.add(thing);
# }
#
# public void removeThing(COS_JThing thing) {
# content.remove(thing);
# }
# }
class COS_JRoom () (field super-ref | make-cell 0) (method new | set! $super-ref | (COS_JNamed) $this) (method super | ? x | (get! $super-ref) $x) (method unknown | ? x | self super $x) (field content | cell new 0) (field doors | cell new 0) (method <init>-V (lambda () | let ((vars | cell new | make-hash | vector (pair 0 $self)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm aload 0) ((= $x 1) | jvm invokespecial <init>-V 0 0) ((= $x 2) | jvm aload 0) ((= $x 3) | jvm new $COS_JList) ((= $x 4) | jvm dup) ((= $x 5) | jvm invokespecial <init>-V 0 0) ((= $x 6) | jvm putfield content $COS_JList) ((= $x 7) | jvm aload 0) ((= $x 8) | jvm new $COS_JList) ((= $x 9) | jvm dup) ((= $x 10) | jvm invokespecial <init>-V 0 0) ((= $x 11) | jvm putfield doors $COS_JList) ((= $x 12) | jvm return) (jvm return)) ) (method <init> | self <init>-V) (method get-COS_JList (lambda () | let ((vars | cell new | make-hash | vector (pair 0 $self)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm aload 0) ((= $x 1) | jvm getfield content $COS_JList) ((= $x 2) | jvm areturn) (jvm return)) ) (method get | self get-COS_JList) (method getDoors-Iterator (lambda () | let ((vars | cell new | make-hash | vector (pair 0 $self)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm aload 0) ((= $x 1) | jvm getfield doors $COS_JList) ((= $x 2) | jvm invokevirtual iterator-Iterator 0 1) ((= $x 3) | jvm areturn) (jvm return)) ) (method getDoors | self getDoors-Iterator) (method addDoor-COS_JDoor-V (lambda (arg0) | let ((vars | cell new | make-hash | vector (pair 0 $self) (pair 1 $arg0)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm aload 0) ((= $x 1) | jvm getfield doors $COS_JList) ((= $x 2) | jvm aload 1) ((= $x 3) | jvm invokevirtual add-Object-V 1 0) ((= $x 4) | jvm return) (jvm return)) ) (method addDoor | self addDoor-COS_JDoor-V) (method addThing-COS_JThing-V (lambda (arg0) | let ((vars | cell new | make-hash | vector (pair 0 $self) (pair 1 $arg0)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm aload 0) ((= $x 1) | jvm getfield content $COS_JList) ((= $x 2) | jvm aload 1) ((= $x 3) | jvm invokevirtual add-Object-V 1 0) ((= $x 4) | jvm return) (jvm return)) ) (method addThing | self addThing-COS_JThing-V) (method removeThing-COS_JThing-V (lambda (arg0) | let ((vars | cell new | make-hash | vector (pair 0 $self) (pair 1 $arg0)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm aload 0) ((= $x 1) | jvm getfield content $COS_JList) ((= $x 2) | jvm aload 1) ((= $x 3) | jvm invokevirtual remove-Object-Z 1 1) ((= $x 4) | jvm pop) ((= $x 5) | jvm return) (jvm return)) ) (method removeThing | self removeThing-COS_JThing-V) ;
65. class translation 'COS_JNamed'
# Produced by Fritzifier, based on JasminVisitor
# Using BCEL library to read Java bytecode
# Here is the original code:
#
# public class COS_JNamed {
# private String name = "-";
# private COS_JWorld world = null;
#
# void setName(String name) {
# this.name = name;
# }
#
# String getName() {
# return name;
# }
#
# void setWorld(COS_JWorld world) {
# this.world = world;
# }
#
# COS_JWorld getWorld() {
# return world;
# }
#
# void update() {
# }
#
# void postUpdate() {
# }
# }
class COS_JNamed () (field super-ref | make-cell 0) (method new | set! $super-ref | (java lang Object) $this) (method super | ? x | (get! $super-ref) $x) (method unknown | ? x | self super $x) (field name | cell new 0) (field world | cell new 0) (method <init>-V (lambda () | let ((vars | cell new | make-hash | vector (pair 0 $self)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm aload 0) ((= $x 1) | jvm invokespecial <init>-V 0 0) ((= $x 2) | jvm aload 0) ((= $x 3) | jvm ldc (String new int-init "-")) ((= $x 4) | jvm putfield name (java lang String)) ((= $x 5) | jvm aload 0) ((= $x 6) | jvm aconst_null) ((= $x 7) | jvm putfield world $COS_JWorld) ((= $x 8) | jvm return) (jvm return)) ) (method <init> | self <init>-V) (method setName-String-V (lambda (arg0) | let ((vars | cell new | make-hash | vector (pair 0 $self) (pair 1 $arg0)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm aload 0) ((= $x 1) | jvm aload 1) ((= $x 2) | jvm putfield name (java lang String)) ((= $x 3) | jvm return) (jvm return)) ) (method setName | self setName-String-V) (method getName-String (lambda () | let ((vars | cell new | make-hash | vector (pair 0 $self)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm aload 0) ((= $x 1) | jvm getfield name (java lang String)) ((= $x 2) | jvm areturn) (jvm return)) ) (method getName | self getName-String) (method setWorld-COS_JWorld-V (lambda (arg0) | let ((vars | cell new | make-hash | vector (pair 0 $self) (pair 1 $arg0)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm aload 0) ((= $x 1) | jvm aload 1) ((= $x 2) | jvm putfield world $COS_JWorld) ((= $x 3) | jvm return) (jvm return)) ) (method setWorld | self setWorld-COS_JWorld-V) (method getWorld-COS_JWorld (lambda () | let ((vars | cell new | make-hash | vector (pair 0 $self)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm aload 0) ((= $x 1) | jvm getfield world $COS_JWorld) ((= $x 2) | jvm areturn) (jvm return)) ) (method getWorld | self getWorld-COS_JWorld) (method update-V (lambda () | let ((vars | cell new | make-hash | vector (pair 0 $self)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm return) (jvm return)) ) (method update | self update-V) (method postUpdate-V (lambda () | let ((vars | cell new | make-hash | vector (pair 0 $self)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm return) (jvm return)) ) (method postUpdate | self postUpdate-V) ;
66. class translation 'COS_JWorld'
# Produced by Fritzifier, based on JasminVisitor
# Using BCEL library to read Java bytecode
# Here is the original code:
#
# import java.util.Iterator;
#
# public class COS_JWorld {
# private COS_JHashMap content;
# private COS_JList inventory;
#
# public COS_JWorld() {
# content = new COS_JHashMap();
# inventory = new COS_JList();
# }
#
# public void add(COS_JNamed named, String name) {
# named.setName(name);
# content.put(named.getName(),named);
# inventory.add(named);
# }
#
# public COS_JNamed get(String name) {
# return (COS_JNamed)content.get(new String(name));
# }
#
# public void update() {
# for (Iterator i = inventory.iterator(); i.hasNext(); ) {
# COS_JNamed o = (COS_JNamed) i.next();
# o.update();
# }
# for (Iterator i = inventory.iterator(); i.hasNext(); ) {
# COS_JNamed o = (COS_JNamed) i.next();
# o.postUpdate();
# }
# }
# }
class COS_JWorld () (field super-ref | make-cell 0) (method new | set! $super-ref | (java lang Object) $this) (method super | ? x | (get! $super-ref) $x) (method unknown | ? x | self super $x) (field content | cell new 0) (field inventory | cell new 0) (method <init>-V (lambda () | let ((vars | cell new | make-hash | vector (pair 0 $self)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm aload 0) ((= $x 1) | jvm invokespecial <init>-V 0 0) ((= $x 2) | jvm aload 0) ((= $x 3) | jvm new $COS_JHashMap) ((= $x 4) | jvm dup) ((= $x 5) | jvm invokespecial <init>-V 0 0) ((= $x 6) | jvm putfield content $COS_JHashMap) ((= $x 7) | jvm aload 0) ((= $x 8) | jvm new $COS_JList) ((= $x 9) | jvm dup) ((= $x 10) | jvm invokespecial <init>-V 0 0) ((= $x 11) | jvm putfield inventory $COS_JList) ((= $x 12) | jvm return) (jvm return)) ) (method <init> | self <init>-V) (method add-COS_JNamed-String-V (lambda (arg0 arg1) | let ((vars | cell new | make-hash | vector (pair 0 $self) (pair 1 $arg0) (pair 2 $arg1)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm aload 1) ((= $x 1) | jvm aload 2) ((= $x 2) | jvm invokevirtual setName-String-V 1 0) ((= $x 3) | jvm aload 0) ((= $x 4) | jvm getfield content $COS_JHashMap) ((= $x 5) | jvm aload 1) ((= $x 6) | jvm invokevirtual getName-String 0 1) ((= $x 7) | jvm aload 1) ((= $x 8) | jvm invokevirtual put-Object-Object-V 2 0) ((= $x 9) | jvm aload 0) ((= $x 10) | jvm getfield inventory $COS_JList) ((= $x 11) | jvm aload 1) ((= $x 12) | jvm invokevirtual add-Object-V 1 0) ((= $x 13) | jvm return) (jvm return)) ) (method add | self add-COS_JNamed-String-V) (method get-String-COS_JNamed (lambda (arg0) | let ((vars | cell new | make-hash | vector (pair 0 $self) (pair 1 $arg0)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm aload 0) ((= $x 1) | jvm getfield content $COS_JHashMap) ((= $x 2) | jvm new (java lang String)) ((= $x 3) | jvm dup) ((= $x 4) | jvm aload 1) ((= $x 5) | jvm invokespecial <init>-String-V 1 0) ((= $x 6) | jvm invokevirtual get-Object-Object 1 1) ((= $x 7) | jvm checkcast $COS_JNamed) ((= $x 8) | jvm areturn) (jvm return)) ) (method get | self get-String-COS_JNamed) (method update-V (lambda () | let ((vars | cell new | make-hash | vector (pair 0 $self)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm aload 0) ((= $x 1) | jvm getfield inventory $COS_JList) ((= $x 2) | jvm invokevirtual iterator-Iterator 0 1) ((= $x 3) | jvm astore 1) ((= $x 4) | jvm aload 1) ((= $x 5) | jvm invokeinterface hasNext-Z 0 1 1) ((= $x 6) | jvm ifeq 14) ((= $x 7) | jvm aload 1) ((= $x 8) | jvm invokeinterface next-Object 0 1 1) ((= $x 9) | jvm checkcast $COS_JNamed) ((= $x 10) | jvm astore 2) ((= $x 11) | jvm aload 2) ((= $x 12) | jvm invokevirtual update-V 0 0) ((= $x 13) | jvm goto 4) ((= $x 14) | jvm aload 0) ((= $x 15) | jvm getfield inventory $COS_JList) ((= $x 16) | jvm invokevirtual iterator-Iterator 0 1) ((= $x 17) | jvm astore 1) ((= $x 18) | jvm aload 1) ((= $x 19) | jvm invokeinterface hasNext-Z 0 1 1) ((= $x 20) | jvm ifeq 28) ((= $x 21) | jvm aload 1) ((= $x 22) | jvm invokeinterface next-Object 0 1 1) ((= $x 23) | jvm checkcast $COS_JNamed) ((= $x 24) | jvm astore 2) ((= $x 25) | jvm aload 2) ((= $x 26) | jvm invokevirtual postUpdate-V 0 0) ((= $x 27) | jvm goto 18) ((= $x 28) | jvm return) (jvm return)) ) (method update | self update-V) ;
67. class translation 'COS_JRobo'
# Produced by Fritzifier, based on JasminVisitor
# Using BCEL library to read Java bytecode
# Here is the original code:
#
# import java.util.Iterator;
#
# public class COS_JRobo extends COS_JThing {
# private COS_JHashMap times;
# private int now;
#
# public COS_JRobo() {
# times = new COS_JHashMap();
# now = 1;
# }
#
# public void update() {
# COS_JRoom location = getRoom();
# //System.out.println("Updating robo...");
# if (location!=null) {
# int oldestTime = now;
# COS_JDoor oldestDoor = null;
# for (Iterator i = location.getDoors(); i.hasNext(); ) {
# COS_JDoor door = (COS_JDoor) i.next();
# //System.out.println(" scanning door ");
# Integer t = (Integer)times.get(door);
# int v = 0;
# if (t!=null) {
# v = t.intValue();
# }
# if (v<oldestTime) {
# oldestTime = v;
# oldestDoor = door;
# }
# }
# if (oldestDoor!=null) {
# times.put(oldestDoor,new Integer(now));
# setNextRoom(oldestDoor.apply(location));
# }
# }
# now++;
# }
# }
#
class COS_JRobo () (field super-ref | make-cell 0) (method new | set! $super-ref | (COS_JThing) $this) (method super | ? x | (get! $super-ref) $x) (method unknown | ? x | self super $x) (field times | cell new 0) (field now | (int) new) (method <init>-V (lambda () | let ((vars | cell new | make-hash | vector (pair 0 $self)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm aload 0) ((= $x 1) | jvm invokespecial <init>-V 0 0) ((= $x 2) | jvm aload 0) ((= $x 3) | jvm new $COS_JHashMap) ((= $x 4) | jvm dup) ((= $x 5) | jvm invokespecial <init>-V 0 0) ((= $x 6) | jvm putfield times $COS_JHashMap) ((= $x 7) | jvm aload 0) ((= $x 8) | jvm iconst 1) ((= $x 9) | jvm putfield now $int) ((= $x 10) | jvm return) (jvm return)) ) (method <init> | self <init>-V) (method update-V (lambda () | let ((vars | cell new | make-hash | vector (pair 0 $self)) (stack | cell new | vector)) | state-machine $vars $stack | ? jvm | ? x | cond ((= $x 0) | jvm aload 0) ((= $x 1) | jvm invokevirtual getRoom-COS_JRoom 0 1) ((= $x 2) | jvm astore 1) ((= $x 3) | jvm aload 1) ((= $x 4) | jvm ifnull 57) ((= $x 5) | jvm aload 0) ((= $x 6) | jvm getfield now $int) ((= $x 7) | jvm istore 2) ((= $x 8) | jvm aconst_null) ((= $x 9) | jvm astore 3) ((= $x 10) | jvm aload 1) ((= $x 11) | jvm invokevirtual getDoors-Iterator 0 1) ((= $x 12) | jvm astore 4) ((= $x 13) | jvm aload 4) ((= $x 14) | jvm invokeinterface hasNext-Z 0 1 1) ((= $x 15) | jvm ifeq 41) ((= $x 16) | jvm aload 4) ((= $x 17) | jvm invokeinterface next-Object 0 1 1) ((= $x 18) | jvm checkcast $COS_JDoor) ((= $x 19) | jvm astore 5) ((= $x 20) | jvm aload 0) ((= $x 21) | jvm getfield times $COS_JHashMap) ((= $x 22) | jvm aload 5) ((= $x 23) | jvm invokevirtual get-Object-Object 1 1) ((= $x 24) | jvm checkcast (java lang Integer)) ((= $x 25) | jvm astore 6) ((= $x 26) | jvm iconst 0) ((= $x 27) | jvm istore 7) ((= $x 28) | jvm aload 6) ((= $x 29) | jvm ifnull 33) ((= $x 30) | jvm aload 6) ((= $x 31) | jvm invokevirtual intValue-I 0 1) ((= $x 32) | jvm istore 7) ((= $x 33) | jvm iload 7) ((= $x 34) | jvm iload 2) ((= $x 35) | jvm if_icmpge 40) ((= $x 36) | jvm iload 7) ((= $x 37) | jvm istore 2) ((= $x 38) | jvm aload 5) ((= $x 39) | jvm astore 3) ((= $x 40) | jvm goto 13) ((= $x 41) | jvm aload 3) ((= $x 42) | jvm ifnull 57) ((= $x 43) | jvm aload 0) ((= $x 44) | jvm getfield times $COS_JHashMap) ((= $x 45) | jvm aload 3) ((= $x 46) | jvm new (java lang Integer)) ((= $x 47) | jvm dup) ((= $x 48) | jvm aload 0) ((= $x 49) | jvm getfield now $int) ((= $x 50) | jvm invokespecial <init>-I-V 1 0) ((= $x 51) | jvm invokevirtual put-Object-Object-V 2 0) ((= $x 52) | jvm aload 0) ((= $x 53) | jvm aload 3) ((= $x 54) | jvm aload 1) ((= $x 55) | jvm invokevirtual apply-COS_JRoom-COS_JRoom 1 1) ((= $x 56) | jvm invokevirtual setNextRoom-COS_JRoom-V 1 0) ((= $x 57) | jvm aload 0) ((= $x 58) | jvm dup) ((= $x 59) | jvm getfield now $int) ((= $x 60) | jvm iconst 1) ((= $x 61) | jvm iadd) ((= $x 62) | jvm putfield now $int) ((= $x 63) | jvm return) (jvm return)) ) (method update | self update-V) ;
68. test JRoom, JDoor, JThing, etc
define s (? x | String new int-init | x);
define door12 (COS_JDoor new <init> (room1) (s "south") (room2) (s "north"));
act | jworld add (thing1) | s "bus";
act | jworld add (robo1) | s "autobus";
act | jworld add (room1) | s "boston";
act | jworld add (room2) | s "newyork";
begin (room1 get add (room1)) (= 1 | room1 get size);
equal "newyork" | door12 apply (room1) (s "south") getName intValue;
equal "boston" | door12 apply (room2) (s "north") getName intValue;
define o (? x | jworld get | s | x);
= "newyork" | (o "bus") getRoom getName intValue;
equal "boston" | (o "autobus") getRoom getName intValue;
equal "newyork" | (o "autobus") getRoom getName intValue;